CESO2025-决赛解析

本文档为 2024-2025 学年全国中学生地球科学奥林匹克竞赛决赛试题的解析与讨论，需要注意它们不是竞赛组委会的参考答案与评分细则，内容的正确性也无法完全保证，故仅供参考。考虑到决赛题目的难度，我们采用专栏探讨的形式进行 W4-W31 题的解析，因此本文档实际上包含六个部分，五个章节：

• CESO2025 决赛参考答案与评分细则
• 第一章 　选择题与地质图识别
• 第二章 　综合问题一：大气动力学
• 第三章 　综合问题二：天体物理中的转动惯量
• 第四章 　综合问题三：地球系统科学中的铈元素
• 第五章 　综合问题四：古生物学研究方法

点击超链接即可直达。若访问不了，说明正在编写中。

目前的问题：Hexo站内使用的mathjax无法正确渲染复杂的公式。

笔者的邮箱：lant.xmu@gmail.com 。如有任何建议，欢迎反馈。

选择题（69分）

Q1	Q2	Q3	Q4	Q5	Q6	Q7	Q8
B	A	A	C	C	D	A	BD
Q9	Q10	Q11	Q12	Q13	Q14	Q15	Q16
C	B	C	AC	ABC	C	ABD	D
Q17	Q18	Q19	Q20	Q21	Q22	Q23	Q24
A	B	C	D	ABCD	C	B	C
Q25	Q26	Q27	Q28	Q29	Q30	Q31	Q32
A	B	C	C	D	D	B	BD
Q33	Q34	Q35	Q36	Q37	Q38	Q39	Q40
C	BC	AC	ABC	B	C	A	ABD

其中，Q1-Q11题每个正确选项2分；Q12-Q40题每个正确选项1分。

2025年7月，竞赛组委会已公布官方答案，上面的是已经修正过的。具体讨论参见子章节。

W1-W3 地质图识别（20分）

W1（10分）

地层接触关系：古生代（P、C、D）与中生代（K、J、T）地层间有明显角度不整合，中生代地层（如T、J、K）间为平行接触，表明沉积环境稳定。新生代（E、N、Q）与中生代间为平行不整合，可能因长期侵蚀，如三叠系上统（T3）覆盖中统（T2）无角度变化（3分）。

地质体：地区中央有侵入岩体，位于志留纪（S）和泥盆纪（D），呈垂直侵入；南部有褶皱构造，志留纪（S）和泥盆纪（D）形成向斜和背斜（2分）。

地质现象：多条断层穿过侵入岩体和古生代地层，含正断层和逆断层。侵入岩体周围和褶皱顶部有侵蚀，地层缺失或变薄；古生代至新生代地层依次沉积，反映沉积环境演变（2分）。

发育顺序：地区先沉积古生代地层，再沉积中生代地层。古生代末至中生代早期形成褶皱构造。褶皱后，岩浆侵入形成侵入岩体，伴随地壳运动形成断层。断层稳定后沉积中生代地层，最后沉积新生代地层，形成现今地貌（3分）。

W2（6分）

角岩、大理岩、石英岩、矽卡岩、片麻岩、麻粒岩。（1点2分，任答3点满分）

W3（4分）

形成年代：石炭纪之后、三叠纪之前。（2分）

理由：γ花岗岩侵入地层最晚到石炭纪，表明其形成晚于石炭纪。同时，其被三叠纪地层覆盖，说明形成早于三叠纪。（2分）

W4-W9 大尺度大气动力学（45分）

W4（8分）

$$
v=\Omega a\cos\phi+u
$$

$$
L=vr=va\cos\phi
$$

$$
\implies L=(\Omega a \cos \phi+u)\cdot a \cos \phi =const… \text{(2分)}
$$

带入赤道（$u=0$）数据，由角动量守恒得：
$$
L=L_0=\Omega a \cdot a=\Omega a^2
$$

$$
\Omega a^2=\Omega a^2 \cos ^2 \phi +ua \cos \phi
$$

$$
u(\phi)=\frac{\Omega a^2 -\Omega a^2 \cos ^2 \phi}{a \cos \phi}
= \frac{\Omega a -\Omega a \cos ^2 \phi}{\cos \phi}
=\boxed{\frac{\Omega a\sin^2\phi}{\cos \phi}}… \text{(6分)}
$$

$$
u(20^\circ)\approx57 \mathrm{m/s};\quad u(30^\circ)\approx 134 \mathrm{m/s}… \text{(8分)}
$$

W5（4分）

$$
\tau(\phi)=\frac{u(\phi)}{H}=\frac{\Omega a \sin^2\phi}{H\cos \phi}… \text{(2分)}
$$

$$
\tau(20^\circ)\approx4.83\times 10^{-3}\mathrm{s^{-1}};\quad \tau(30^\circ)\approx1.12\times 10^{-2}\mathrm{s^{-1}}… \text{(4分)}
$$

W6（10分）

对$\tau(\phi)$ 采用小角近似（题目里用的是$\Delta$，但考虑到科学性，应该用$\partial$）：
$$
\frac{\partial u}{\partial z} = \frac{\Omega y^2}{aH} = \frac{-g}{T_0 \cdot 2 \Omega \cdot (y/a)} \cdot \frac{\partial T}{\partial y} = - \frac{ag}{yT_0 \cdot 2\Omega} \cdot \frac{\partial T}{\partial y}… \text{(2分)}
$$

$$
\frac{\partial T}{\partial y} = \frac{\Omega g^2}{aH} \cdot \frac{yT_0 \cdot 2 \Omega}{ag}
= - \frac{2\Omega^2 T_0}{a^2 g H} y^3… \text{(4分)}
$$

两边积分：
$$
T_{M} = - \frac{\Omega^2 T_0}{2a^2 g H} y^4 + k… \text{(8分)}
$$

其中 $k=T_{M_{0}}$ 表征哈德利环流情况下的赤道温度。…(10分)

W7（2分）

$$
T_E(0)=T_0+\frac{1}{3}\Delta T… \text{(2分)}
$$

W8（6分）

阴影部分表征赤道地区因哈德利环流向高纬输送的热量（2分），满足关系式：
$$
\int_{y_c}^{y_a} [T(M) - T(E)] y_x \mathrm{d}y + \int_{y_b}^{y_d} [T(M) - T(E)] y_x \mathrm{d}y = \int_{y_a}^{y_b} [T(E) + T(M)] y_x \mathrm{d}y
$$
等号左边表征哈德利环流给高纬方向带来的热量，等号右边表征哈德利环流在赤道带走的热量（2分）。

左右两极的交点表征哈德利环流的南北界；中间的两个交点表征热量输送态的变化（2分）。

W9（15分）

将辐射平衡温度的表达式套用小角近似：
$$
T_E(\phi) = \underbrace{T_{0} + \frac{1}{3}\Delta T}{T{E0}} - \Delta T \cdot \left(\frac{y}{a}\right)^2
$$

$$
\implies T_E=-\frac{\Delta Ty^2}{a^2}+T_{E0}… \text{(2分)}
$$

$$
\because \quad T_{M} = - \frac{\Omega^2 T_0}{2a^2 g H} y^4 + T_{M0}
$$

因此边界条件即为$T_E$与$T_M$的联立：
$$
-\frac{\Delta Ty^2}{a^2}+T_{E0}=- \frac{\Omega^2 T_0}{2a^2 g H} y^4 + T_{M0}
$$
由于净加热为零：
$$
\int_0^Y T_M \mathrm{d}y = \int_0^Y T_E \mathrm{d}y
$$
左边：
$$
\begin{align}
\int_0^Y T_M(y) \mathrm{d}y &= \int_0^Y \left( T_{M0} - \frac{\Omega^2 T_0}{2 a^2 g H} y^4 \right) \mathrm{d}y \
&= T_{M0} y - \frac{\Omega^2 T_0}{2 a^2 g H} \frac{y^5}{5} \Bigg|0^Y \
&= T{M0} Y - \frac{\Omega^2 T_0}{10 a^2 g H} Y^5
\end{align}
$$
右边：
$$
\begin{align}
\int_0^Y T_E(y) \mathrm{d}y &= \int_0^Y \left( T_{E0} - \frac{\Delta T}{a^2} y^2 \right) \mathrm{d}y \
&= T_{E0} y - \frac{\Delta T}{a^2} \frac{y^3}{3}\Bigg|0^Y \
&= T{E0} Y - \frac{\Delta T}{3 a^2} Y^3
\end{align}
$$
回代：
$$
T_{M0} - \frac{\Omega^2 T_0}{10 a^2 g H} Y^4 = T_{E0} - \frac{\Delta T}{3 a^2} Y^2… \text{(6分)}
$$
联立边界条件和净加热积分：
$$
\left( T_{M0} - \frac{\Omega^2 T_0}{2 a^2 g H} Y^4 \right) - \left( T_{M0} - \frac{\Omega^2 T_0}{10 a^2 g H} Y^4 \right)
= \left( T_{E0} - \frac{\Delta T}{a^2} Y^2 \right) - \left( T_{E0} - \frac{\Delta T}{3 a^2} Y^2 \right)
$$

$$
\implies \quad \frac{\Omega^2 T_0}{a^2 g H} \left( -\frac{4}{10} \right) Y^4 = \frac{\Delta T}{a^2} \left( -\frac{2}{3} \right) Y^2
$$

$$
i.e. \quad\boxed { Y =\sqrt \frac{5 \Delta T g H}{3 \Omega^2 T_0} }… \text{(8分)}
$$

下面求赤道地区的温度差：

$$
T_{E0} - T_{M0} = \frac{\Delta T}{a^2} Y^2 - \frac{\Omega^2 T_0}{2 a^2 g H} Y^4… \text{(10分)}
$$

$$
Y^2 = \frac{5 \Delta T g H}{3 \Omega^2 T_0}, \quad Y^4 = \left( \frac{5 \Delta T g H}{3 \Omega^2 T_0} \right)^2
$$

$$
T_{E0} - T_{M0} = \frac{\Delta T}{a^2} \left( \frac{5 \Delta T g H}{3 \Omega^2 T_0} \right) - \frac{\Omega^2 T_0}{2 a^2 g H} \left( \frac{25 \Delta T^2 g^2 H^2}{9 \Omega^4 T_0^2} \right)
$$

$$
T_{E0} - T_{M0} = \frac{5 \Delta T^2 g H}{3 a^2 \Omega^2 T_0} - \frac{25 \Delta T^2 g H}{18 a^2 \Omega^2 T_0} = \frac{30 \Delta T^2 g H - 25 \Delta T^2 g H}{18 a^2 \Omega^2 T_0}
$$
即：
$$
\boxed{T_{E0} - T_{M0} = \frac{5 \Delta T^2 g H}{18 a^2 \Omega^2 T_0}}… \text{(13分)}
$$
带入数据，得 Y≈3797.8 km，$T_{E0} - T_{M0}$ ≈ 5.92 K。…（15分）

W10-W15 转动惯量反演天体构造（35分）

W10（5分）

AC

W11（4分）

0（R=0）；1（r=R=1）。

W12（6分）

$$
M=\rho V=\frac{4}{3}\pi R^3 \rho
$$

根据补充知识②：
$$
V=SR\Rightarrow \mathrm{d}V=4\pi R^2 \mathrm{d}r
$$
带入补充知识①：
$$
\mathrm{d}I=\frac{8\pi \rho}{3}R^4 \mathrm{d}r…\text{(2分)}
$$
两边积分：
$$
I=\int^R_0{\frac{8\pi \rho}{3}R^4 \mathrm{d}r}=\frac{8\pi \rho}{15}R^5…\text{(4分)}
$$
因为$\rho=\frac{3M}{4\pi R^3}$，带入上式：
$$
I=\frac{2}{5}MR^2
$$
所以：
$$
\lambda_0=\frac{I}{MR^2}=\frac{2}{5}…\text{(6分)}
$$

W13（8分）

内外两层的角标分别为1和2，不妨设V为1个单位：
$$
M_1=\rho_1V_1=2\rho \cdot \frac{4}{3}\pi (R/3)^3= \frac{8}{81}\pi R^3 \rho
$$
其中R是星球的总半径，ρ是外层的密度。
$$
M_2=\rho(V-V_1)=\frac{104}{81}\pi R^3 \rho
$$

$$
M=M_1+M_2=\frac{112}{81}\pi R^3 \rho
$$

$$
\overline{\rho}=\frac{M}{\frac{4}{3}\pi R^3}=\frac{28}{27}\rho
$$

内核是实心球体，适用于W12求出的转动惯量公式：
$$
I_1=\frac{2}{5}M_1R^2_1=\frac{16}{3645}\pi\rho R^5…\text{(2分)}
$$
外层是厚球壳，求其转动惯量需要用薄球壳的积分。
$$
\mathrm{d}I=\frac{2}{3}r^2\mathrm{d}m=\frac{2}{3}r^2p\mathrm{d}V=\frac{2}{3}r^2\cdot{(4\pi\rho r^2\mathrm{d}r)}
$$
$$
I_2=\int \mathrm{d}I= \frac{8\pi\rho}{3}\int_a^b r^4\mathrm{d}r=\frac{8\pi\rho}{3}\cdot\frac{r^5}{5}\Bigg|^b_a=\frac{8\pi\rho}{15}(b^5-a^5)
$$

$$
M_2=\rho \cdot \frac{4}{3}\pi (b^3-a^3) \Rightarrow \rho =\frac{3M_2}{4\pi(b^3-a^3)}
$$

回代入 $I_2$ 的表达式：
$$
I_2=\frac{2}{5}\cdot M_2\cdot \frac{b^5-a^5}{b^3-a^3}
$$
这就是任意厚球壳的转动惯量表达式，其中M是质量，b是外圈半径，a是内圈半径。带入上面的条件：
$$
I_2 = \frac{2}{5} \cdot \frac{104\pi \rho R^3}{81} \cdot \frac{R^5 - (R/3)^5}{R^3 - (R/3)^3} = \frac{1936}{3645} \pi \rho R^5…\text{(4分)}
$$

$$
I=I_1+I_2=\frac{1952}{3645}
$$

$$
\lambda_1=\frac{I}{MR^2}=\frac{122}{315}\approx0.387<\lambda_0…\text{(6分)}
$$

这是因为虽然内核的密度高，但半径小，所以星球的质量分布整体更靠近中心，导致转动惯量因子小于均匀实心球体。…（8分）

W14（6分）

内外两层的角标分别是c（ore）和m（antle），地球相关的角标是E（arth），内核1220km，外核5151km。

$$
M_c = \frac{4}{3} \pi R_c^3 \rho_c
$$

$$
M_m = \frac{4}{3} \pi (R_E^2 - R_c^3) \rho_m
$$

$$
M = \frac{4}{3} \pi [\rho_c R_c^3 + \rho_m (R_E^3 - R_c^3)]…\text{(2分)}
$$

$$
I_c = \frac{8 \pi}{15} \rho_c R_c^5
$$

$$
I_m = \int_{R_c}^{R_E} \frac{2}{3} r^2 \cdot \rho_m \cdot 4 \pi R^2 \mathrm{d}r = \frac{8 \pi}{15} \rho_m (R_E^5 - R_c^5)
$$

$$
\lambda_2=\frac{I_c+I_m}{MR_E^2} = \frac{\frac{8 \pi}{15} [\rho_c R_c^5 + \rho_m (R_E^5 - R_c^5)]}{\frac{4}{3} \pi [\rho_c R_c^3 + \rho_m (R_E^3 - R_c^3)] R_E^2}
$$

$$
\lambda_2= \frac{2}{5} \cdot \frac{\rho_c R_E^5 +\rho_m R_E^5 - \rho_m R_c^5}{\rho_c R_c^3 + \rho_m R_E^3 - \rho_m R_c^3} R_E^2 = 0.33…\text{(4分)}
$$

$$
\rho_c / \rho_m = \beta\enspace\Rightarrow\enspace \rho_c = \beta \rho_m
$$

$$
\Rightarrow \lambda_2 = \frac{2}{5} \cdot \frac{\beta \rho_m R_E^5 + \rho_m R_E^5 - \rho_m R_c^5}{(\beta\rho_m R_c^3 + \rho_m R_c^3 - \rho_m R_c^3) R_E^2}= \frac{2}{5} \cdot \frac{(\beta-1) R_c^5 + R_E^5}{R_E^2[(\beta-1) R_c^3 + R_E^3]}=0.33
$$

统一量纲，带入所有数据，求解方程，立即得：

$$
\Rightarrow \beta \approx 32.614…\text{(6分)}
$$

即地球内核与外层的密度比约为 32.614。

W15（6分）

内外两层的角标分别为1和2，沿用W13的解题思路：

• 内核密度 $\rho_1 = 2\rho$，外层密度 $\rho$
• 总半径 $R$，内核半径 $r_1$（设 $x = \frac{r_1}{R}$）

$$
m_1 = \rho_1 V_1 = 2\rho \cdot \frac{4}{3}\pi r_1^3 = \frac{8}{3}\pi\rho x^3 R^3
$$

$$
m_2 = \rho V_2 = \rho_s \left( \frac{4}{3}\pi R^3 - \frac{4}{3}\pi r_2^3 \right) = \frac{4}{3}\pi\rho R^3 (1 - x^3)
$$

$$
M = m_1 + m_2 = \frac{4}{3}\pi\rho R^3 (1 + x^3)
$$

$$
I_1 = \frac{2}{5} m_1 r_1^1 = \frac{16}{15}\pi\rho x^5 R^5
$$

$$
I_2 = \frac{2}{5}\cdot m_2\cdot \frac{b^5-a^5}{b^3-a^3}=\frac{8\pi\rho}{15} (R^5 - r_1^5) = \frac{8\pi\rho}{15} R^5 (1 - x^5)
$$

$$
I = I_1 + I_2 = \frac{8\pi\rho}{15} R^5 (1 + x^5)…\text{(2分)}
$$

$$
\lambda(x) = \frac{I}{M R^2} = \frac{\frac{8}{15} \pi\rho R^5 (1 + x^5)}{\frac{4}{3}\pi\rho R^5 (1 + x^3)} = \frac{2}{5} \cdot \frac{1 + x^5}{1 + x^3},\enspace x\in(0,1)…\text{(4分)}
$$

对 $\lambda(x) $ 求导，令其导数为 0 ，等价于求解微分方程（可以直接使用 CASIO ClassWiz fx-991 CN CW 的解方程功能运算，需要设定x=1为初值。）
$$
\frac{\mathrm{d}}{\mathrm{d}x}\left(\ \frac{2}{5} \cdot \frac{1 + x^5}{1 + x^3}\right)\Bigg|_{x=x}=0,\enspace x \in(0,1)
$$

得 $x\approx 0.722=x_0$，因为 $x\to0, \lambda(x)\to 0.4;x\to1, \lambda(x)\to 0.4>\lambda(x_0)\approx0.348$，所以 λ 在 (0, x₀) 上单调递减， (x₀, 1) 上单调递增，x₀ 就是极小值点。

因此，当内核的半径约为 0.722 倍行星的半径时，该行星的转动惯量因子最小。此时的转动惯量因子约为0.348。…（6分）

W16-W23 稀土元素（55分）

W16（3分）

ⅢB-4、ⅢB-5、ⅢB-6。（1点1分）

W17（10分）

本题的化学计算流程如下图所示。其中高亮的部分是题目给出的数值。

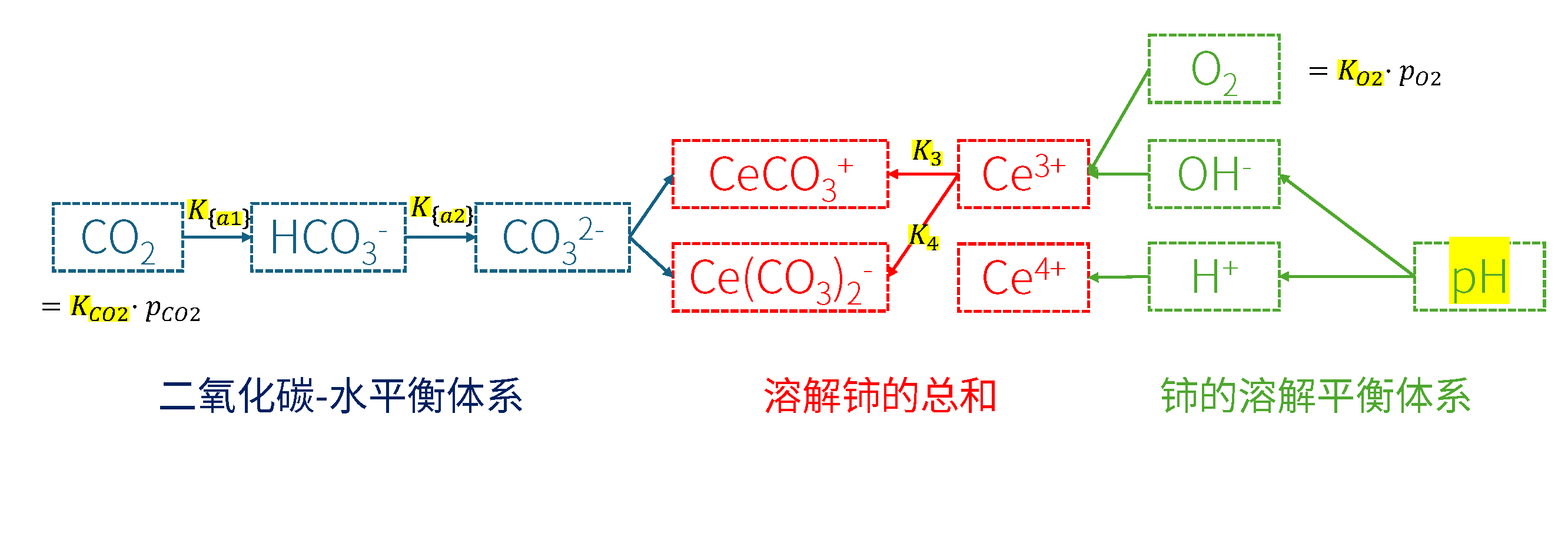
$$
\ce {\sum [Ce]=[Ce^{3+}] +[Ce^{4+}] + [CeCO^+_3] +[Ce(CO_3)^-_2]}
$$

$$
\ce{[pH]}=-\lg [\ce{H^+}]\Rightarrow \ce{[H+]}=7.94 \times 10^{-9}\enspace \text{mol/L}
$$

$$
[\ce{OH-}] = \frac{K_w}{[\ce{H+}]} = \frac{10^{-14}}{7.94 \times 10^{-9}} = 1.259 \times 10^{-6} , \text{mol/L}…\text{(2分)}
$$

$$
[\ce{O2}] = K_{H,\ce{O2}} \cdot p_{\ce{O2}} = 0.00125 \times \underbrace{0.21}_{\mathrm{present\ oxygen \ content}}= 2.625 \times 10^{-4} , \text{mol/L}
$$

$$
\ce{[Ce^{3+}]=\frac{1}{K_1 \cdot [O_2]^{1/4} \cdot [OH^-]^3}}=1.57 \times 10^{-21} \enspace \text{mol/L}…\text{(4分)}
$$

$$
\ce{[Ce^{4+}]=\frac{[H^+]^4}{K_2}}=2.88 \times 10^{-41} \enspace \text{mol/L}…\text{(5分)}
$$

$$
\ce{[CO_2]} = K_{H,CO_2} \cdot p_{\mathrm{CO_2}}=0.033 \times \underbrace{420 \times 10^{-6}}_{\mathrm{present\ CO_2 \ content}}=1.386 \times 10^{-5} \enspace \text{mol/L}
$$

$$
K_{a1}=\frac{[\mathrm{H}^+][\mathrm{HCO}_3^-]}{[\mathrm{H}_2\mathrm{CO}_3]}\Rightarrow[\mathrm{HCO}3^-]=\frac{K{a1}[\mathrm{H}_2\mathrm{CO}3]}{[\mathrm{H}^+]}=\frac{K{a1}[\mathrm{CO}_2]}{[\mathrm{H}^+]}=7.79 \times 10^{-4}\enspace \text{mol/L}
$$

$$
K_{a2}=\frac{[\mathrm{H}^{+}][\mathrm{CO}{3}^{2-}]}{[\mathrm{HCO}{3}^{-}]}\Rightarrow[\mathrm{CO}{3}^{2-}]=\frac{K{a2}[\mathrm{HCO}_{3}^{-}]}{[\mathrm{H}^{+}]}=4.59 \times 10^{-6} \enspace \text{mol/L}
$$

$$
\ce{[CeCO^+_3]=K_3 [Ce^{3+}][CO}_3^{2-}] =2.94 \times 10^{-19}\enspace \text{mol/L}…\text{(8分)}
$$

$$
\ce{[Ce(CO_3)^-_2]=K_4 [Ce^{3+}][CO}_3^{2-}]^2 =1.12 \times 10^{-14}\enspace \text{mol/L}…\text{(9分)}
$$

$$
\ce {\sum [Ce]=[Ce^{3+}] +[Ce^{4+}] + [CeCO^+_3] +[Ce(CO_3)^-_2]}=1.12\times 10^{-14}\enspace \text{mol/L} \approx \boxed{10^{-14} \enspace \text{mol/L}}…\text{(10分)}
$$

W18（5分）

AF（南海的溶解氧一般是饱和的，需要论文数据支撑，否则D也可以选。）

W19（3分）

放大误差；排除干扰；方便（质谱仪）检测（1点1分）。

W20（3分）

B（3分）

W21（6分）

Pr 和 Nd 是 Ce 的直接相邻元素，适合插值估算 $\ce{Ce/Ce^*}$（3分）；La 非直接相邻，有微弱异常，降低精度（3分）。

W22（10分）

计算三个样本的 $\ce{Ce/Ce^}$：
$$
\ce{[Ce/Ce^]_1=\frac{5.203}{64}\times\frac{\frac{2.389}{26}}{(\frac{0.5574}{7.1})^2}}\approx1.21\ \text{ppm},\quad \sum REE=10.5854
$$

$$
\ce{[Ce/Ce^*]_2=\frac{5.404}{64}\times\frac{\frac{2.675}{26}}{(\frac{0.6901}{7.1})^2}}\approx0.92\ \text{ppm},\quad \sum REE=9.2441
$$

$$
\ce{[Ce/Ce^*]_3=\frac{5.632}{64}\times\frac{\frac{2.756}{26}}{(\frac{0.6617}{7.1})^2}}\approx1.07\ \text{ppm},\quad \sum REE=12.1667
$$

所以，样本2的 $\ce{Ce/Ce^}$ 负偏，样本1和3的$\ce{Ce/Ce^}$ 正偏，偏离程度：1>3。…（3分）

• 样本1的Ce异常富集，说明样本1的沉积环境偏还原，可能在近海潟湖区域沉积，有着较高的沉积速率，阻滞了Ce³⁺ 的氧化。ΣREE中等，陆源输入量一般；…（5分）

• 样本2的Ce异常亏损，说明形成于氧气较充足的浅海环境，Ce³⁺ 部分氧化为 Ce⁴⁺，形成 CeO₂ 沉淀或被铁锰氧化物吸附移除。ΣREE最少，说明沉积地离大陆较远；…（8分）

• 样本3的Ce略富集，说明形成于氧化与还原条件交界的浅海环境，Ce³⁺ 部分保留，部分氧化为 Ce⁴⁺，氧化过程不完全。ΣREE最多，说明此地陆源碎屑输入丰富，沉积速率高。…（10分）

W23（15分）

先导出相关的热力学关系式：
$$
\ce{[Ce^{3+}]=\frac{1}{K_1 \cdot [O_2]^{1/4} \cdot [OH^-]^3}}=\frac{1}{K_1 \cdot( K_{H,\ce{O2}} \cdot p_{\ce{O2}})^{1/4} \cdot [OH^-]^3}\propto p^{-1/4}_{O_2}
$$

$$
\ce{
\begin{aligned}
\sum [Ce] &= [Ce^{3+}] + [Ce^{4+}] + [CeCO^{3+}] + [Ce(CO3)^{2-}] \
&\approx [Ce^{3+}] + [CeCO^{3+}] + [Ce(CO3)^{2-}] \
&= [Ce^{3+}] + K_3 [Ce^{3+}][CO3^{2-}] + K_4 [Ce^{3+}][CO3^{2-}]^2 \
&= [Ce^{3+}]\cdot \underbrace{(1 + K_3 [CO3^{2-}] + K_4 [CO3^{2-}]^2)}_{const.}
\end{aligned}
}
$$

$$
\implies \ce{Ce/Ce^* \propto \sum [Ce] \propto p^{-1/4}_{O_2}}
$$

$$
i.e. \quad p_{O_2}=p_{O_2PAL}\cdot \left( \frac{k}{Ce/Ce^*} \right)^4
$$

其中：k是目前全球海水平均的 $\ce{Ce/Ce^*}$ ，$p_{O_2PAL}$ 是目前的氧气分压，约等于0.21。…(8分)

考虑到后期成岩改造会使得 $\ce{Ce/Ce^}$ 升高，导致反演出现偏差，因此同一时期内应选择较低的 $\ce{Ce/Ce^}$ 数据。（比如白云岩化作用等，参见 Liu 等, 2019）

作图略。

【15分：样本点选取12分（GOE的缓慢上升、NOE的上升端点，1个1分；选取较低的样本数据2分）；端点值的计算、绘制15分】

下面给出一个结合实测 $\ce{Ce/Ce^*}$ 数据作出的图表：

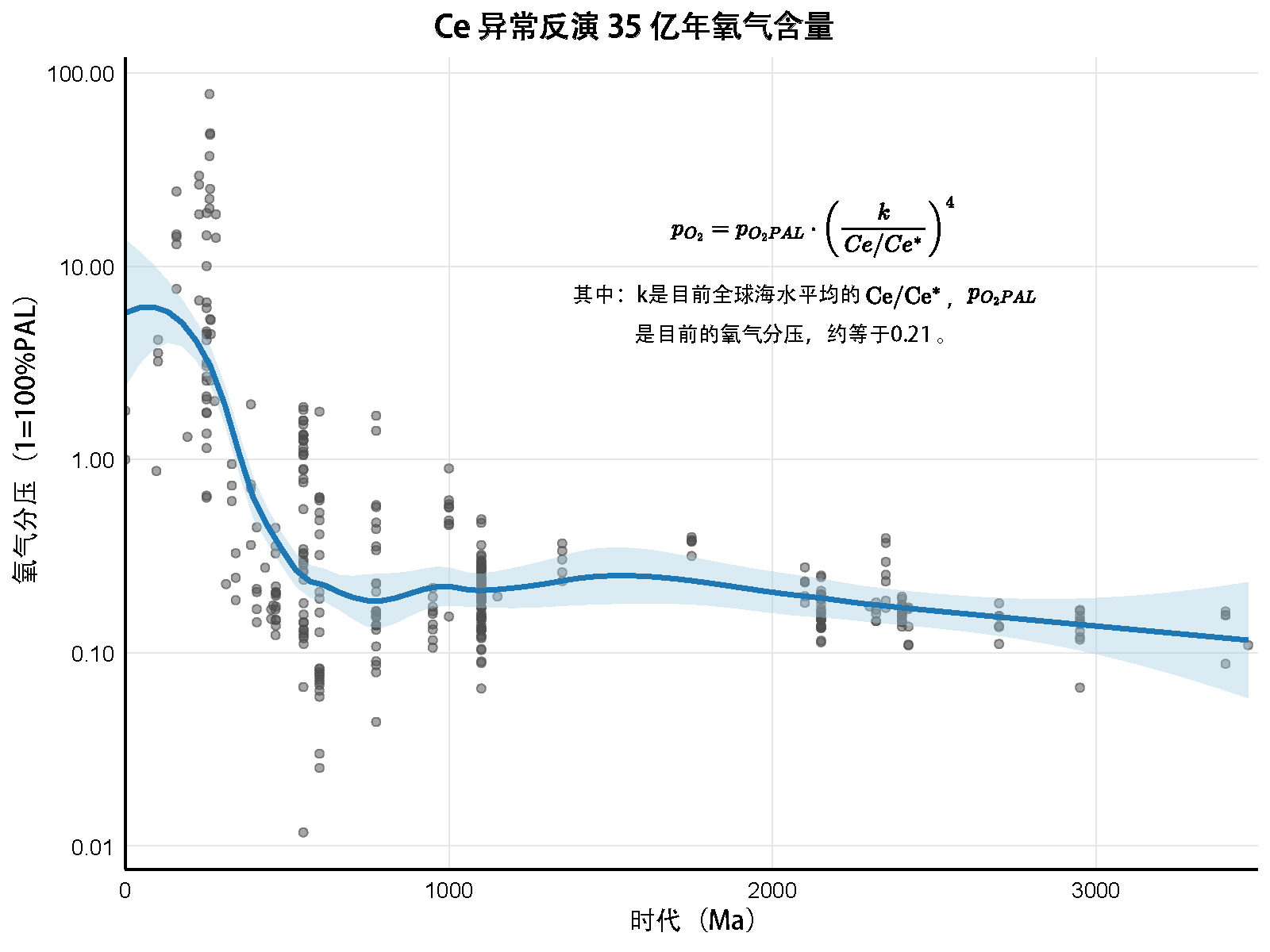
图a 铈异常反演出的35亿年以来的氧气含量变化图，拟合线通过LOESS（局部加权回归）绘制，阴影部分示 95% 置信区间，纵轴采用了对数刻度。 $\ce{Ce/Ce^*}$ 数据及对应时间从 Liu 等（2021）处取得，样本系未进行数据筛选的沉积碳酸盐岩样品（共350个数据点，其中242个石灰岩，84个白云岩和24个未分类）。

本图的优点是样本数量大，在较长的地史年代中能保持较好的拟合（精确性较好），但缺点是趋势的准确性不足（比如PTB后的下降趋势未能很好地反映，且高估了PTB前的氧气含量。当然这也可能是由于PTB后的样本不足）。

对该组数据更为详尽的讨论参见专栏3或原论文，csv文件可在笔者的repository中取得。

图b 铈异常反演出的 27 亿年以来的氧气含量变化图，拟合线通过LOESS（局部加权回归）绘制，阴影部分示 95% 置信区间，纵轴采用了对数刻度。 $\ce{Ce/Ce^}$ 数据及对应时间从 Liu 等（2021）处取得，样本系对图a的结果进行了数据筛选（data filtering）的数据，但由于样本数量较小（以 100 Ma 为间隔，取第10百分位数后仅有 24 组数据），虽然在显生宙时期能保持较好的拟合趋势（准确性较好），但在更长的时间尺度上缺乏*精确性，正如原论文所言 “This method improves time resolution, but results in greater uncertainties.”。若需更为精确的图表，更多数据点应包含在内。

这两幅图使用 R 语言绘制，代码文件亦可在笔者的 repository 中找到。

W24-W31 古生物学回归分析 35分

W24 （4分）

标本编号	hm/fm	由hm/fm判定的性别	dh/ds	由dh/ds判定的性别
H01	1.18	M	1.95	M
H02	1.15	M	2.40	M
H03	1.18	M	1.18	F
H04	1.23	M	2.19	M
H05	1.23	M	1.33	F
H06	1.19	M	1.63	F
H07	1.00	F	1.36	F
H08	1.09	F	0.86	F
H09	0.90	F	1.71	F
H10	0.98	F	1.20	F
H11	1.15	M	1.90	M
H12	1.05	F	1.07	F
H13	1.00	F	1.45	F
H14	0.92	F	0.87	F
H15	1.16	M	2.00	M
H16	1.14	M	2.00	M

（1列1分，有错误者不得分）

W25 （4分）

自由度：1。

零假设：$dh/hs$ 和 $hm/fm$ 两种比值指标得到的性别结果无关。

列联表：

性别	$dh/hs$ M	$dh/hs$ F	Σ
$hm/fm$ M	6	3	9
$hm/fm$ F	0	7	7
Σ	6	10	n=16

…（2分）
$$
\chi^2=\frac{112}{15}\approx7.467>\chi^2_{0.01}…\text{(3分)}
$$
所以至高在99%的显著性上，零假设不成立。

即根据 $dh/hs$ 和 $hm/fm$ 两种比值指标得到的性别结果，最高有99%的关联性，犯错的概率为1%。…（4分）

W26 （6分）

（提示中给的“统筹规划计算任务”指的是在W26-W28中，相同组的数据合并处理。）

考察幂律方程的一般形式：
$$
y = k \cdot x^\alpha
$$
指数函数不是线性形式，所以我们必须转换为对数后进行线性回归！！！
$$
\ln y = \ln k + \alpha \ln x
$$
这样， $$S_{xx} = \sum (\ln x_i - \bar{x})^2$$, $$S_{yy} = \sum (\ln y_i - \bar{y})^2$$, $$S_{xy} = \sum (\ln x_i - \bar{x})(\ln y_i - \bar{y})$$。

本题中，自由度v=16-2=14，那么若 $$F > F_{0.001}(14) = 17.143$$，幂律关系在 99.9% 显著性水平下成立。…（3分）

(1) fm 对 hm

• $$\bar{\ln(\text{hm})} \approx 2.8347$$, $$\bar{\ln(\text{fm})} \approx 2.7486$$。

• $$S_{xx} \approx 1.332$$, $$S_{yy} \approx 0.727$$, $$S_{xy} \approx 0.9525$$。

• $$\hat{\beta_1} = \frac{S_{xy}}{S_{xx}} \approx 0.7147$$, $$R^2 = \frac{S_{xy}^2}{S_{xx}S_{yy}} \approx 0.937$$。

• $$F = \frac{0.937}{1 - 0.937} \cdot 14 \approx 207.49> 17.143$$。

  所以 fm 对 hm 的幂律关系在 99.9% 显著性水平下成立。…（4分）

(2) hs 对 dh

• $$\bar{\ln(\text{dh})} \approx 1.420$$, $$\bar{\ln(\text{hs})} \approx 1.016$$。

• $$S_{xx} \approx 2.592$$, $$S_{yy} \approx 1.016$$, $$S_{xy} \approx 1.037$$。

• $$\hat{\beta_1} \approx 0.4$$, $$R^2 \approx 0.4082$$。

• $$F = \frac{0.4082}{1 - 0.4082} \cdot 14 \approx 9.6586< 17.143$$。

    所以 hs 对 dh 的幂律关系在 99.9% 显著性水平下不成立。...（5分）
  

(3) ul 对 rd

• $$\bar{\ln(\text{rd})} \approx 2.119$$, $$\bar{\ln(\text{ul})} \approx 2.085$$。

• $$S_{xx} \approx1.4686$$, $$S_{yy} \approx 1.3980$$, $$S_{xy} \approx 1.4132$$。

• $$\hat{\beta_1} \approx 0.962$$, $$R^2 \approx 0.972$$。

• $$F = \frac{0.972}{1 - 0.972} \cdot 14 \approx 500> 17.143$$。

    所以 ul 对 rd 的幂律关系在 99.9% 显著性水平下成立。
  

综上所述，fm 对 hm 和 ul 对 rd 适用幂律方程；hs 对 dh 不适用幂律方程。…（6分）

W27 （6分）

等速生长意味着标度幂指数 $$\alpha = 1$$。这里我们需要使用 t 检验判断线性回归得到的斜率 $$\hat{\beta_1}$$ 是否显著偏离零假设 $$\beta_1 = 1$$，在 80% 显著性水平下比较 t 值与临界值 $$t_{0.2}(v)$$。若 $$|t| < t_{0.2}(14) = 1.345$$，则无法拒绝零假设，符合等速生长。

(1) fm 对 hm

使用 W26 结果：$$\hat{\beta_1} \approx 0.7147$$, $$R^2 \approx 0.937$$, $$S_{xx} \approx 1.332$$, $$S_{yy} \approx 0.727$$, $$n = 16$$。计算 SSE：
$$
\text{SSE} = (1 - R^2) \cdot S_{yy} \approx 0.0459
$$
计算 t 值：
$$
t = \frac{0.946 - 1}{\sqrt{\frac{0.0459}{14 \cdot 1.332}} }\approx-5.75
$$
$$|t| = 5.75 > 1.345$$，零假设不成立，fm 对 hm 不符合等速生长。…（3分）

(2) hs 对 dh

使用 W26 结果：$$\hat{\beta_1} \approx 0.4$$, $$R^2 \approx 0.611$$, $$S_{xx} \approx 2.592$$, $$S_{yy} \approx 1.1067$$, $$n = 16$$。计算 SSE：
$$
\text{SSE} = (1 - R^2) \cdot S_{yy} \approx 0.0459
$$
计算 t 值：
$$
t = \frac{0.4 - 1}{ \sqrt{\frac{0.5926}{14 \cdot 2.592}}} \approx -4.7
$$
$$|t| = 4.7 > 1.345$$，零假设不成立，hs 对 dh 不符合等速生长。

综上所述，fm 对 hm 、hs 对 dh 都不符合等速生长。…（6分）

W28 （4分）

这两题需要将雄性标本和雌性标本分类讨论，所以我们整理如下数据：

标本编号	性别（M:x; F:y）	dh	hs	hm	fm
H01	M	7.8	4.0	26.0	22.0
H02	M	6.0	2.5	23.0	20.0
H04	M	7.0	3.2	27.0	22.0
H06	M	6.5	4.0	21.5	18.0
H11	M	3.8	2.0	15.0	13.0
H15	M	7.0	3.5	22.0	19.0
M组的平均数	$\bar{x}$	6.35	3.2	22.42	19.00
M组的方差	$s_x$	1.338	0.806	4.248	3.346
H03	F	4.0	3.0	19.5	17.0
H05	F	4.0	3.0	18.5	15.0
H07	F	3.0	2.2	12.5	12.5
H08	F	3.0	3.5	19.0	17.5
H09	F	3.6	2.1	13.0	14.5
H10	F	2.4	2.0	11.0	11.2
H12	F	3.2	3.0	16.8	16.0
H13	F	2.9	2.0	12.0	12.0
H14	F	2.0	2.3	11.0	12.0
H16	F	5.0	2.5	16.0	14.0
F组的平均数	$\bar{y}$	3.31	2.56	14.93	14.93
F组的方差	$s_y$	0.885	0.532	3.316	3.316

(1) dh

$$
t = \frac{6.35 - 3.31}{\sqrt{\frac{1.338^2}{6} + \frac{0.885^2}{10}}} \approx 4.951
$$

$$
v \approx \frac{\left( \frac{1.338^2}{6} + \frac{0.885^2}{10} \right)^2}{\frac{\left( \frac{1.338^2}{6} \right)^2}{5} + \frac{\left( \frac{0.885^2}{10} \right)^2}{9}} \approx 7.66
$$

取 $$v \approx 8$$，$$t_{0.01}(8) = 3.355$$。$$|t| = 4.951 > 3.355$$，dh 具有性双形现象。…（1分）

(2) hs

$$
t = \frac{3.20 - 2.56}{\sqrt{\frac{0.806^2}{6} + \frac{0.532^2}{10}}} \approx 1.734
$$

$$
v \approx \frac{(0.108 + 0.028)^2}{\frac{0.108^2}{5} + \frac{0.028^2}{9}} \approx 7.64
$$

取 $$v \approx 8$$，$$t_{0.01}(8) = 3.355$$。$$|t| = 1.734 < 3.355$$，hs 不具有性双形现象。…（2分）

(3) hm

$$
t = \frac{22.42 - 14.93}{\sqrt{\frac{4.248^2}{6} + \frac{3.316^2}{10}}} \approx \frac{7.49}{\sqrt{3.008 + 1.099}} \approx 3.695
$$

$$
v \approx \frac{(3.008 + 1.099)^2}{\frac{3.008^2}{5} + \frac{1.099^2}{9}} \approx 8.67
$$

取 $$v \approx 9$$，$$t_{0.01}(9) = 3.250$$。$$|t| = 3.695 > 3.250$$，hm 具有性双形现象。…（3分）

(4) fm

$$
t = \frac{19.00 - 14.17}{\sqrt{\frac{3.346^2}{6} + \frac{2.163^2}{10}}} \approx 3.161
$$

$$
v \approx \frac{(1.867 + 0.468)^2}{\frac{1.867^2}{5} + \frac{0.468^2}{9}} \approx 7.56
$$

取 $$v \approx 8$$，$$t_{0.01}(8) = 3.355$$。$$|t| = 3.161 < 3.355$$，fm 不具有性双形现象。

综上所述，dh 和 hm 在 99% 显著性水平下具有性双形现象，hs 和 fm 在 99% 显著性水平下不具有性双形现象。 …（4分）

W29 （6分）

据题，此处的自由度为$v = (n_1 - 2) + (n_2 - 2) = n_1 + n_2 - 4=12$，若 $$C > C_{0.1}(12)=2.807$$，则在 90% 显著性水平下，幂律关系表现出性双形现象。

(1) fm 对 hm

M ($ n_1 = 6 $)：

• $ \ln(\overline{\mathrm{hm}}) \approx 3.076 $, $ \ln(\overline{\mathrm{fm}}) \approx 2.936 $

• $ S_{xx} \approx 0.251 $, $ S_{yy} \approx 0.219 $, $ S_{xy} \approx 0.234 $

• $ \hat{\beta_1} \approx 0.932 $, $ R^2 \approx 0.996 $, $ SSE_1 = (1 - 0.996) \cdot 0.219 \approx 0.000876 $

F ($ n_2 = 10 $)：

• $ \ln(\overline{\mathrm{hm}}) \approx 2.484 $, $ \ln(\overline{\mathrm{fm}}) \approx 2.389 $

• $ S_{xx} \approx 0.336 $, $ S_{yy} \approx 0.240 $, $ S_{xy} \approx 0.287 $

• $ \hat{\beta_1} \approx 0.854 $, $ R^2 \approx 0.963 $, $ SSE_2 = (1 - 0.963) \cdot 0.240 \approx 0.00888 $.

**合并 ($ n = 16 $)：**使用 W26 结果：$ S_{yy} \approx 0.727 $, $ R^2 \approx 0.937 $, $ SSE_0 = (1 - 0.937) \cdot 0.727 \approx 0.0459 $
$$
C = \frac{\frac{0.0459 - (0.000876 + 0.00888)}{2}}{\frac{0.000876 + 0.00888}{16 - 4}} =\frac{6024}{271} \approx 22.22
$$

$ C = 22.22 > 2.807 $，fm 对 hm 的幂律关系在 90% 显著性水平下表现出性双形现象。 …（3分）

(2) hs 对 dh

M ($ n_1 = 6 $)：

• $ \ln(\overline{\mathrm{dh}}) \approx 1.811 $, $ \ln(\overline{\mathrm{hs}}) \approx 1.101 $

• $ S_{xx} \approx 0.138 $, $ S_{yy} \approx 0.106 $, $ S_{xy} \approx 0.077 $

• $ \hat{\beta_1} \approx 0.558 $, $ R^2 \approx 0.524 $, $ SSE_1 = (1 - 0.524) \cdot 0.106 \approx 0.0505 $

F ($ n_2 = 10 $)：

• $ \ln(\overline{\mathrm{dh}}) \approx 1.108 $, $ \ln(\overline{\mathrm{hs}}) \approx 0.981 $

• $ S_{xx} \approx 0.235 $, $ S_{yy} \approx 0.149 $, $ S_{xy} \approx 0.112 $

• $ \hat{\beta_1} \approx 0.477 $, $ R^2 \approx 0.362 $, $ SSE_2 = (1 - 0.362) \cdot 0.149 \approx 0.0950 $

**合并 ($ n = 16 $)：**使用 W26 结果：$ S_{yy} \approx 1.016 $, $ R^2 \approx 0.4082 $, $ SSE_0 = (1 - 0.4082) \cdot 1.016 \approx 0.5926 $

$$
C = \frac{\frac{0.5926 - (0.0505 + 0.0950)}{2}}{\frac{0.0505 + 0.0950}{16 - 4}} = \frac{8942}{485} \approx 18.44
$$

$ C = 18.44 > 2.807 $，hs 对 dh 的幂律关系在 90% 显著性水平下表现出性双形现象。

综上所述，在 90% 显著性水平下，fm 对 hm 和 hs 对 dh 的幂律关系均表现出性双形现象。 …（6分）

附：使用最大似然估计也可得到同样的结论，下面给出了可在 R 中实现的代码。

library(maxLik)

data <- data.frame(
  lnx = c(3.258096538, 3.135494216, 2.970414466, 3.295836866, 2.917770732, 
          3.068052935, 2.525728644, 2.944438979, 2.564949357, 2.397895273, 
          2.708050201, 2.821378886, 2.48490665, 2.397895273, 3.091042453, 
          2.772588722),
  lny = c(3.091042453, 2.995732274, 2.833213344, 3.091042453, 2.708050201, 
          2.890371758, 2.525728644, 2.862200881, 2.674148649, 2.415913778, 
          2.564949357, 2.772588722, 2.48490665, 2.48490665, 2.944438979, 
          2.63905733)
)

data_m <- data[1:6, ]
data_f <- data[7:16, ]

# 针对 fm 对 hm 和 hs 对 dh 分别进行 MLE

# (1) fm 对 hm
loglik_restricted_fm <- function(params) {
  beta0 <- params[1]
  beta1 <- params[2]
  sigma <- params[3]
  resid_m <- data_m$lny - (beta0 + beta1 * data_m$lnx)
  resid_f <- data_f$lny - (beta0 + beta1 * data_f$lnx)
  -sum(dnorm(resid_m, mean = 0, sd = sigma, log = TRUE)) -
    sum(dnorm(resid_f, mean = 0, sd = sigma, log = TRUE))
}
fit_restricted_fm <- maxLik(loglik_restricted_fm, start = c(beta0 = 0, beta1 = 1, sigma = 1))
ll_restricted_fm <- -fit_restricted_fm$maximum

loglik_unrestricted_fm <- function(params) {
  beta0_m <- params[1]; beta1_m <- params[2]; sigma_m <- params[ Nort3]
  beta0_f <- params[4]; beta1_f <- params[5]; sigma_f <- params[6]
  resid_m <- data_m$lny - (beta0_m + beta1_m * data_m$lnx)
  resid_f <- data_f$lny - (beta0_f + beta1_f * data_f$lnx)
  -sum(dnorm(resid_m, mean = 0, sd = sigma_m, log = TRUE)) -
    sum(dnorm(resid_f, mean = 0, sd = sigma_f, log = TRUE))
}
fit_unrestricted_fm <- maxLik(loglik_unrestricted_fm, start = c(0, 1, 1, 0, 1, 1))
ll_unrestricted_fm <- -fit_unrestricted_fm$maximum

lambda_fm <- -2 * (ll_restricted_fm - ll_unrestricted_fm)
p_value_fm <- 1 - pchisq(lambda_fm, df = 2)
cat("fm 对 hm: Lambda =", lambda_fm, ", p-value =", p_value_fm, "\n")
if (lambda_fm > 4.605) {
  cat("fm 对 hm 在 90% 显著性水平下表现出性双形现象。\n")
} else {
  cat("fm 对 hm 在 90% 显著性水平下不表现出性双形现象。\n")
}

# (2) hs 对 dh
loglik_restricted_hs <- function(params) {
  beta0 <- params[1]
  beta1 <- params[2]
  sigma <- params[3]
  resid_m <- data_m$lny - (beta0 + beta1 * data_m$lnx)
  resid_f <- data_f$lny - (beta0 + beta1 * data_f$lnx)
  -sum(dnorm(resid_m, mean = 0, sd = sigma, log = TRUE)) -
    sum(dnorm(resid_f, mean = 0, sd = sigma, log = TRUE))
}
fit_restricted_hs <- maxLik(loglik_restricted_hs, start = c(beta0 = 0, beta1 = 1, sigma = 1))
ll_restricted_hs <- -fit_restricted_hs$maximum

loglik_unrestricted_hs <- function(params) {
  beta0_m <- params[1]; beta1_m <- params[2]; sigma_m <- params[3]
  beta0_f <- params[4]; beta1_f <- params[5]; sigma_f <- params[6]
  resid_m <- data_m$lny - (beta0_m + beta1_m * data_m$lnx)
  resid_f <- data_f$lny - (beta0_f + beta1_f * data_f$lnx)
  -sum(dnorm(resid_m, mean = 0, sd = sigma_m, log = TRUE)) -
    sum(dnorm(resid_f, mean = 0, sd = sigma_f, log = TRUE))
}
fit_unrestricted_hs <- maxLik(loglik_unrestricted_hs, start = c(0, 1, 1, 0, 1, 1))
ll_unrestricted_hs <- -fit_unrestricted_hs$maximum

lambda_hs <- -2 * (ll_restricted_hs - ll_unrestricted_hs)
p_value_hs <- 1 - pchisq(lambda_hs, df = 2)
cat("hs 对 dh: Lambda =", lambda_hs, ", p-value =", p_value_hs, "\n")
if (lambda_hs > 4.605) {
  cat("hs 对 dh 在 90% 显著性水平下表现出性双形现象。\n")
} else {
  cat("hs 对 dh 在 90% 显著性水平下不表现出性双形现象。\n")
}

W30 （2分）

• 根据独立性检验得到二者的相关性极大；

• 二者与成熟算法判断出的结果均保持较高一致性；

• dh 具有显著性别差异（M较大），hs 差异不显著，导致 dh/hs 比值在M中较大，在F中较小，可作为性别判别依据，hm/fm组同理；

• dh 的显著性别差异（W28）与 hs 对 dh 的非等速生长（W27）导致 dh/hs 比值在M中较高，F中较低，显著的幂律关系（W26）支持其作为性别判别依据，hm/fm组同理。

（任答两点2分）

W31 （3分）

考察rd/ul的 $\chi^2$ 检验：

样本	rd/ul	性别	算法性别
H1	1.08	M	M
H2	1.00	F	M
H3	0.94	F	F
H4	1.04	M	M
H5	1.00	F	F
H6	1.05	M	M
H7	1.08	M	F
H8	1.06	M	F
H9	1.17	M	F
H10	1.00	F	F
H11	1.00	F	M
H12	1.07	M	F
H13	1.00	F	F
H14	1.00	F	F
H15	1.10	M	M
H16	1.00	F	M

此处的阈值取50百分位数。

零假设：通过rd/ul和算法得到的性别结果无关，列联表如下：

性别	$rd/ul$ M	$rd/ul$ F	Σ
算法 M	4	3	7
算法 F	4	5	9
Σ	8	8	n=16

$$
\chi^2=\frac{16}{63}\approx0.25
$$

这个值太小了，不足以拒绝零假设（1分）。也就是零假设在取中位数为阈值的情况下不成立，可能有如下几方面原因：一是样本太少了，不具有普遍性；二是阈值的取用需结合更多样本分析。在这种情况下，指标rd/ul 可能是有潜力的，但这还需要结合F-test、T-test等回归分析进行进一步的讨论。（2分）

---

致谢：本文档的预印本公开发表时，小红书用户“小红薯647AAFC5”对部分答案进行了修正，特对他表示感谢！

相关修正：

1. W5 ：$\tau(20^\circ)\approx0.08\mathrm{m/s};\quad \tau(30^\circ)\approx 0.25 \mathrm{m/s}\implies\tau(20^\circ)\approx4.83\times10^{-3}\mathrm{s^{-1}};\quad \tau(30^\circ)\approx1.12\times 10^{-2}\mathrm{s^{-1}}$
2. W7：$T_E(0)=T_0-\frac{2}{3}\Delta T\implies T_E(0)=T_0+\frac{1}{3}\Delta T$
3. W9：数据代入修正为 “ Y≈3797.8 km，$T_{E0} - T_{M0}$ ≈ 5.92 K。”
4. W11：$0;1\implies0(r=R=0);\enspace 1(r=R=1)$。