第二章 综合问题一：大气动力学

$$
\begin{equation*}
Lant
\end{equation*}
$$

$$
\begin{equation*}
\text{Xiamen University}
\end{equation*}
$$

---

摘要：本章提供了对2024-2025学年全国中学生地球科学竞赛决赛试题大气动力学题组（W4-W9，共45分）的讨论。本章聚焦于大尺度大气动力学中，哈德利环流的生消变化及物理机制，并结合部分类地行星的大气进行了比较行星学的实证分析。同时给出了原试题的题目来源。

关键词：CESO、Held-Hou模型、大气动力学、哈德利环流、比较行星学

---

要做一个优秀的科学家，并不需要你总是正确的，重要的是你在当时所能获得的概念和观察资料的基础上，通过合理的推理得出结论。从这个意义上说，亚里士多德和托勒密是伟大的科学家，但在16世纪那些新的事实已经表明他们是错误的时候，仍然重复他们观点的人就不是了。哥白尼在他的日心体系中保留了许多本轮，开普勒相信数字神秘主义，而伽利略坚信行星轨道是完美的圆形，尽管如此，我们仍将他们视为伟大的科学家。同样，哈德利、麦克劳林、康德、拉普拉斯、德吕克等人在历史上也应占有一席之地。但当新的观测和理论已经证明某些解释是错误时，仍然坚持这些解释就不符合科学精神了。（Persson, 2006）

专栏讨论 哈德利环流

我们在高中学过三圈环流（three-cells model），知道三圈环流模型大体上反映了大气环流的基本情况，即由太阳辐射差异引起的赤道和两极之间的温差是引起和维持大气环流的根本原因，地球自转运动产生的地转偏向力（Coriolis Force，亦称科里奥利力，本文统一为高中的习惯表述地转偏向力）使赤道和两极间温差所引起的经向（南北向）环流变为纬向（东西向）环流（图 2.1）。

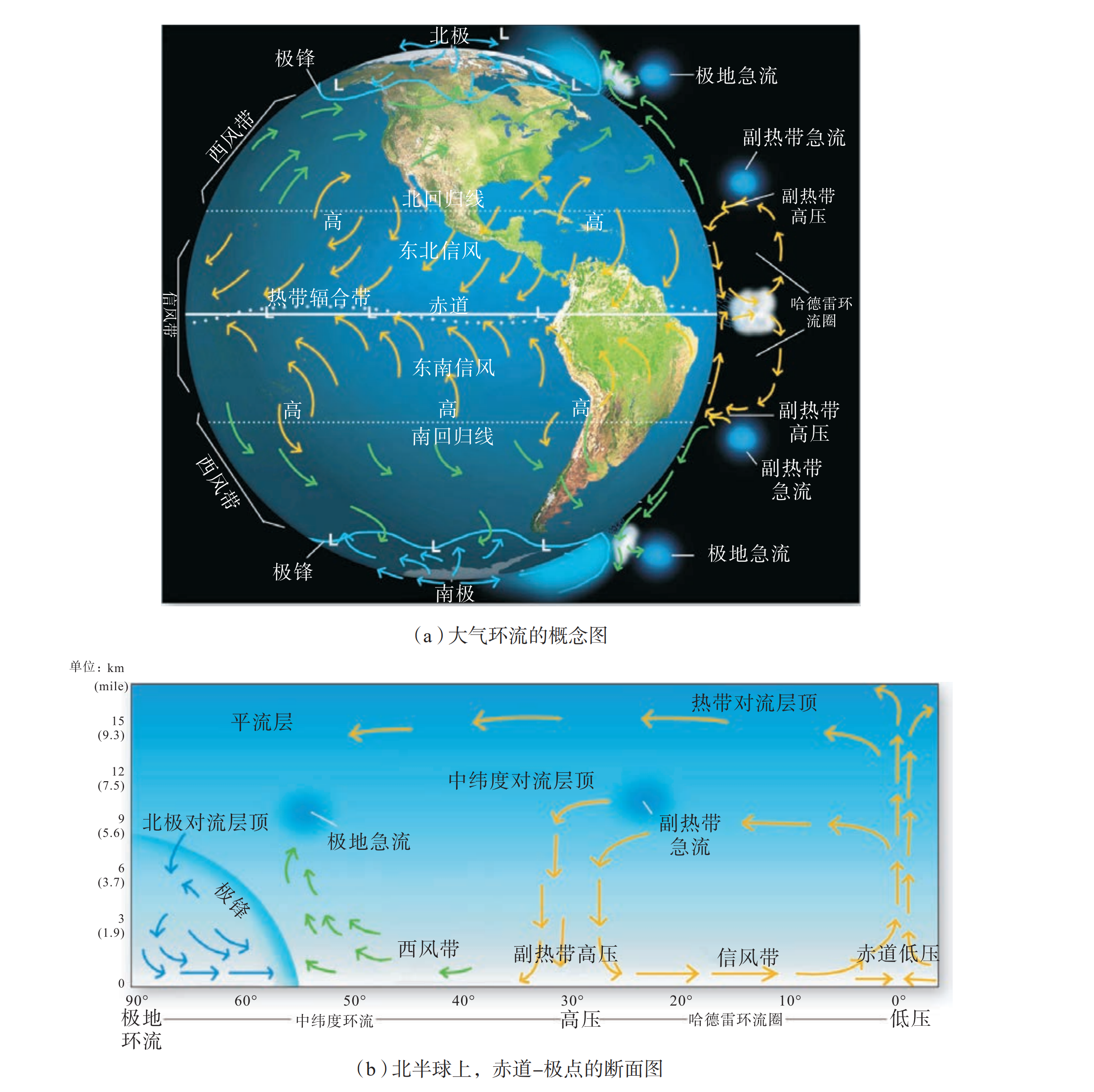
图2.1 大气环流一般模式的两种视图，两个视图都给出了哈德利（雷）环流圈、副热带高压、极锋、副极地低压带、亚热带急流和极地急流的大体位置。（Christopherson R., 2018:167）

在对流层高层，赤道地区因强烈的太阳辐射而升温，暖空气上升，形成低压区（也就是赤道辐合带，ITCZ），吸引周边气流向赤道汇聚。这些气流在向两极运动的过程中，受地转偏向力（科里奥利力）的影响不断向右偏转，大约在北纬30°附近，气流方向逐渐转为西风。由于持续的空气堆积，这一区域对流层中低层气压增高，高空下沉气流因压缩而增温，形成深厚且暖性的副热带高压带。

在经圈方向上，低纬度地区的闭合环流被称为哈德利环流（Hadley Cell），这一环流直接由南北热量差异驱动，是典型的热力环流。哈德利环流通过赤道上升气流和北纬30°附近的下沉气流连接起来，构成了低纬度大气运动的基本框架。同时，副热带高压带（subtropical high）作为哈德利环流的下沉分支，推动近地面气流向极地运动，受地转偏向力右偏，形成了中纬度宽广的西风带，影响全球气候。

北上的暖空气与极地南下的冷空气在北纬60°附近相遇，形成极锋区（polar front），暖空气爬升引发对流，对流层顶形成极锋急流，地面形成副极地低压带（subpolar low），常伴随温带气旋。部分高空暖空气向极地冷却下沉，形成高纬环流；另一部分折返赤道，在北纬30°下沉，构成费雷尔环流，连接副热带高压带与副极地低压带。极地冷空气下沉形成极地高压带，近地面南下气流受地转偏向力形成极地东风带。

由此，我们会自然地提出一个问题：为什么恰好在特定的纬度附近，三圈环流会突然下沉，并在地面辐散，形成一个完整的环流圈呢？有没有一种数学物理方法限定了这种边界？为此，我们需要追溯人类研究这些环流的历史，在更大的背景和视域下研究三圈环流。本章将以三圈环流在热带区域的分项：哈德利环流为例，研究其在行星风系尺度下的形成与变化。

哈德利环流的历史

在十八世纪初，英国两位杰出的科学家——以彗星研究闻名的埃德蒙·哈雷爵士（Sir Edmund Halley ）和乔治·哈德利爵士（Sir George Hadley）——提出了一种概念框架，旨在解释热带地区观测到的风场模式。这些早期尝试综合已知的大尺度大气环流的解释，为如今的低纬经向环流提供了最早的科学解释。这一大尺度的经向环流覆盖了地球一半的区域，其变化影响着数十亿人的生活。与以沃克命名的大尺度纬向热带环流（沃克环流，Walker Circulation）一起，哈德利环流构成了地球能量收支的基本调节机制（Diaz and Bradley, 2004）。

哈德利小史

乔治·哈德利（George Hadley，1685-1768）是一位英国律师和业余气象学家。尽管他的职业生涯主要集中在法律领域，但他在科学领域的贡献，特别是对信风和全球风系的解释，使其成为18世纪科学史上的关键人物。

哈德利1685年出生于伦敦一个富裕家庭，其兄长约翰·哈德利（John Hadley）因发明“哈德利六分仪”而闻名，这也导致乔治的科学贡献长期被误认为是约翰的。作为一位自学成才的科学家，哈德利对气象学表现出了浓厚的兴趣。1735年，他加入了英国皇家学会，负责管理学会的气象工作，包括为海外通讯员提供仪器以及收集和分析欧洲大陆的气象观测数据。这些工作促使他深入思考地表气压和风场变化的地理规律，为其理论的形成奠定了基础。

哈德利于1768年去世，其生平细节因历史记载有限而显得模糊，我们甚至找不到他的标准画像，但他的科学遗产却通过“哈德利环流”得以永存。月球上的“哈德利陨石坑”和英国气象局的“哈德利中心”都以他的名字命名。哈德利的工作不仅反映了18世纪科学探索的精神，也为现代气候和大气科学研究提供了重要的理论基础。

哈德利之前的科学家早已关注到低纬度信风的存在，并对其成因进行了一些有益的讨论。伽利略曾提出，信风源于低纬度地球自转速度较快，大气滞后形成西向风。1685年，哈雷在皇家学会辩论中提出，信风由热带地区昼夜温差驱动，太阳加热位置西移导致空气上升，依质量守恒产生信风。但这一模型因无法解释信风的稳定性而被质疑。

哈德利不满意既有的解释，于 1735 年在 Philosophical Transaction 上发表论文，提出信风由低纬度上升气流驱动。哈德利认为，地球赤道处自转速度最快，极地方向减慢，高纬低动量空气向赤道移动时因动量守恒偏西，上升气流向极地方向偏东后冷却下沉，形成中纬度西风。他的模型假设了覆盖南北半球的大尺度环流，但忽略了季节性和海洋大陆的不对称性，且预测的信风速度过快，需通过地表摩擦解释实际风速。哈德利的理论因缺乏直观性和观测支持，长期未获广泛认可。同期，其他学者如达朗贝尔（Jean le Rond d’Alembert ）、康德（Immanuel Kant）、拉普拉斯（Pierre-Simon Laplace）等人也提出类似风系解释，但均有局限。

19世纪，地转偏向力被确认为大气环流中风矢量偏转的核心机制，取代了哈德利的线性动量守恒假设。哈德利的模型因低估偏转幅度（仅为地转偏向力的一半）而受到质疑，其通过地表摩擦解释风速较低的观点也因高空云运动观测（如30°N附近西南风速远低于理论预测）而被削弱。1899年，威廉·莫里斯·戴维斯（W.M.Davis）在皇家气象学会的演讲中尖锐批评哈德利理论，指出其忽略了气压梯度力与地转偏向力的动态平衡，导致无法全面解释大气过程。

20世纪，气象学家逐渐认识到哈德利环流并非仅由动量守恒驱动，而是涉及复杂的物理过程，包括热力作用、气压分布和地球自转的协同影响。1947年，罗斯贝（Rossby）进一步提出，哈德利环流主要局限于热带地区，作为多单元经向环流的一部分，这一观点与费雷尔1860年提出的三圈环流模型有相似之处，实证了大气环流的复杂性和多尺度特征。（Persson, 2006）

伟大科学家的贡献并非终点，而是通向更精确真理的起点。科学的生命力在于不断修正和超越，以开放的心态接受新证据，摒弃已被证伪的假设。

确定哈德利环流的边界：Held-Hou 模型

在前人工作的基础上，麻省理工学院的 Schneider （1977）对哈德利环流的纬度界限进行了开创性的研究，通过引入非线性动量平流效应和创新的数值方法，显著推进了对全球大气环流尺度的理解。三年后的1980年，普林斯顿大学的 I.M.Held 和哈佛大学的 A.Y.Hou 提出了一个对称模型，重点探讨辐射加热和摩擦通量如何控制哈德利环流的宽度和强度，以及地表风、哈德利和费雷尔环流的特征（Held and Hou, 1980）。模型的核心在于，赤道附近从地表上升的空气在向极地移动时保持其角动量的守恒。这种风的分布反过来决定了温度的分布，而温度分布又通过要求能量守恒来确定环流的纬度范围。这与哈德利最初对环流的构想形成对比，他认为环流延伸至两极。哈德利环流在赤道及其附近产生冷却效应，而在哈德利环流内的高纬度地区则产生增温效应。这种能量输送可以通过适当的垂直稳定性标准化，转化为质量输送（mass transportation），从而确定环流的强度。

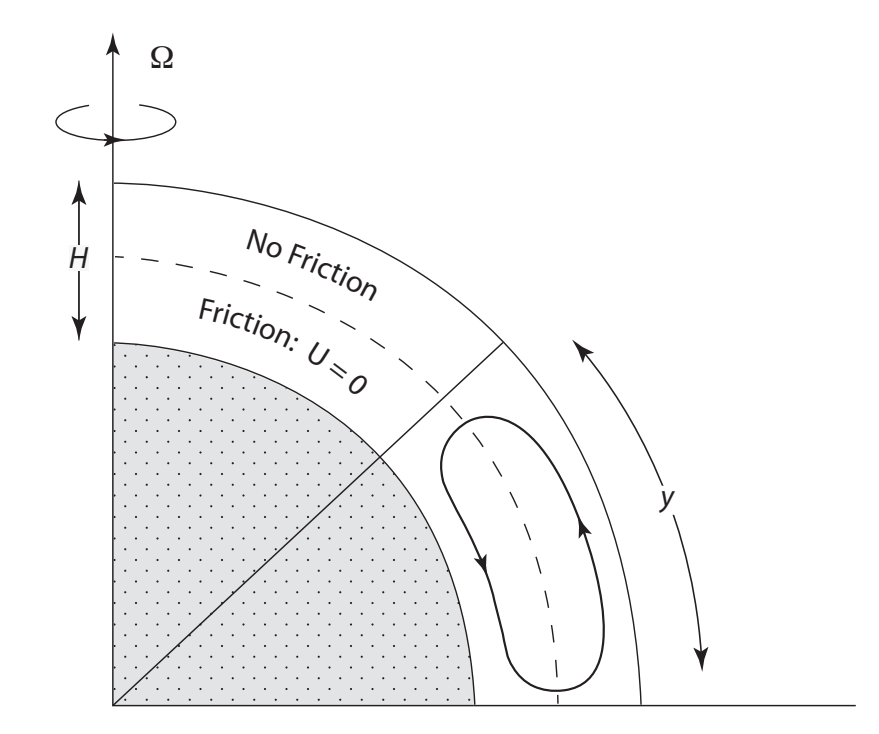
图 2.2 Held-Hou模型的示意图（Lu et al., 2014）

图2.2 给出了Held-Hou模型的示意图。其中，下层受地面摩擦的影响，其内的流动通常较小。在上层中，摩擦效应几乎为零，因此在这个高度，气团在向极地移动时保持其角动量的守恒。对气团的速度进行三向分解，垂直分量为w，纬向分量为u，经向分量为v，那么设这些气团起初在赤道处相对于固体地球的纬向速度u为0，根据角动量守恒（$L=mvr$），我们就可以算出气团在任意纬度的纬向速度。

气团纬向速度的绝对量，由相对于固体地球的纬向分量u，与地球的线速度分量组成：
$$
v=u+\Omega a\cos\phi\tag{2.1}
$$
其中的 $\Omega$ 是地球的自转角速度，$a$ 是地球的半径，$\phi$ 是气团的纬度，$\Omega a\cos\phi$ 就是气团在纬度为$\phi$ 处的线速度（回顾必修二的物理知识，$v=\omega r$）。由于气团的质量为 1 个单位，角动量守恒可如式 2.2 简化：
$$
L=vr=va\cos\phi\tag{2.2}
$$
将式 2.1 带入式 2.2：
$$
L=(\Omega a \cos \phi+u)\cdot a \cos \phi =const.\tag{2.3}
$$
式 2.3 就是适用于本例的角动量守恒，对于任意的纬度，角动量$L$是一个常数，由此带入赤道（$\phi=0,u=0$ ）的数据：
$$
L=L_0=\Omega a \cdot a=\Omega a^2\tag{2.4}
$$

$$
\Omega a^2=\Omega a^2 \cos ^2 \phi +ua \cos \phi\tag{2.5}
$$

整理以得到 $u(\phi)$。
$$
u(\phi)=\frac{\Omega a^2 -\Omega a^2 \cos ^2 \phi}{a \cos \phi}
= \frac{\Omega a -\Omega a \cos ^2 \phi}{\cos \phi}
=\boxed{\frac{\Omega a\sin^2\phi}{\cos \phi}}\tag{2.6}
$$

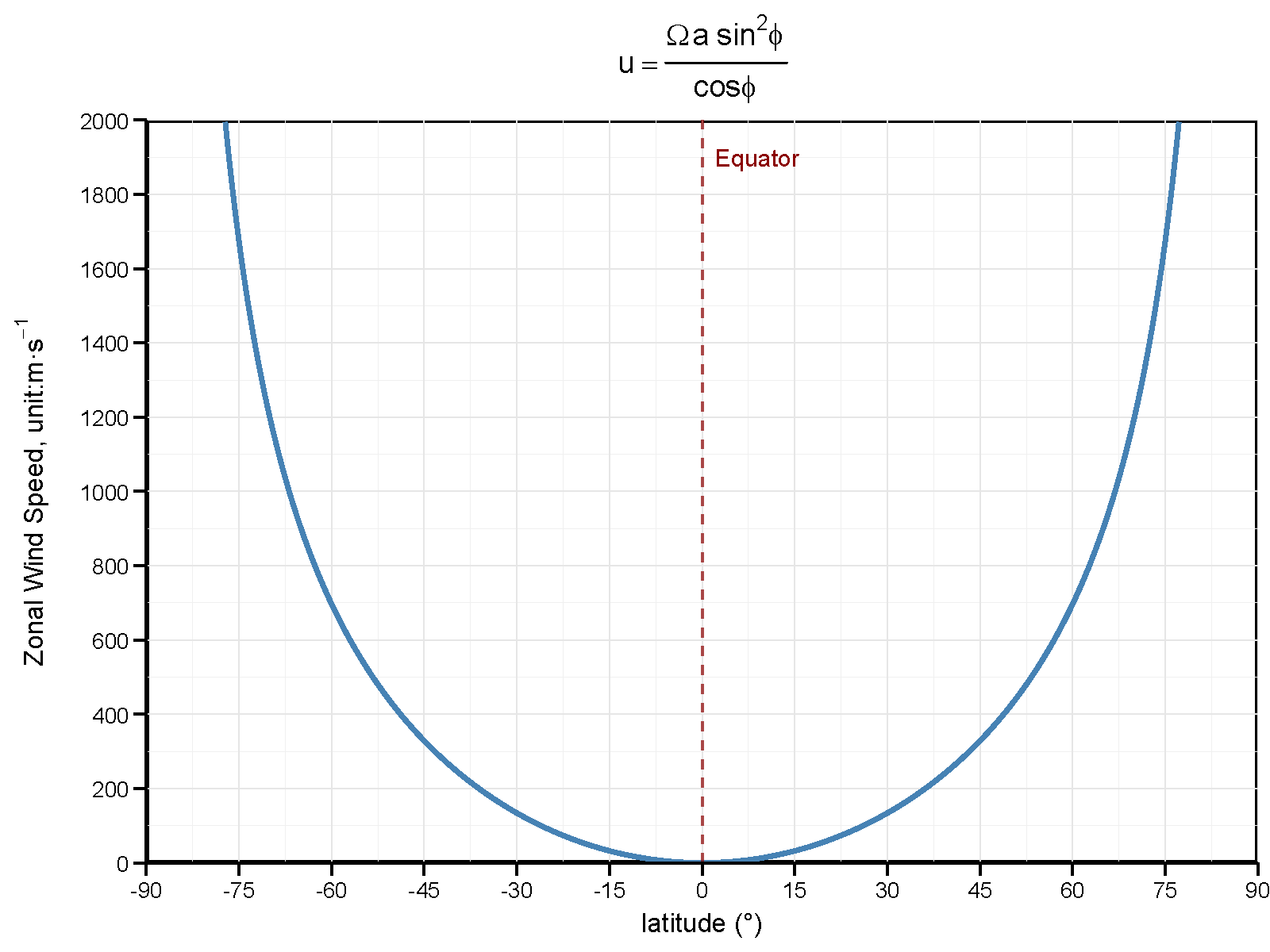
图 2.3 带入$\Omega=7.3\times 10^{-5}\enspace \text{rad/s}, a=6371.4 \enspace\text{km}$，得到$ u(\phi)$ 在$(-90^{\circ},90^{\circ})$的分布。在中高纬地区风速过高，且$\phi \to \pi/2, u\to \infty$，显然不可能。图像使用R语言绘制，源码可在笔者的repository里找到（zonalu.txt）。

图 2.3 绘制了$u(\phi)$ 在$(-90^{\circ},90^{\circ})$的分布。可以看出，尽管角动量守恒显然无法准确描述中高纬度区域的区域风速，但在热带和亚热带上层对流层的风速变化确实呈现出式 2.6 的情形。风速从赤道开始大致以二次方的速度增加，在所谓的副热带急流处达到最大值。同时我们可以绘制出相关的垂向风切变（vertical wind shear，$\tau(\phi)$）随纬度的变化：
$$
\tau(\phi)=\frac{u(\phi)}{H}=\frac{\Omega a \sin^2\phi}{H\cos \phi}=\frac{\partial u}{\partial z}\tag{2.7}
$$

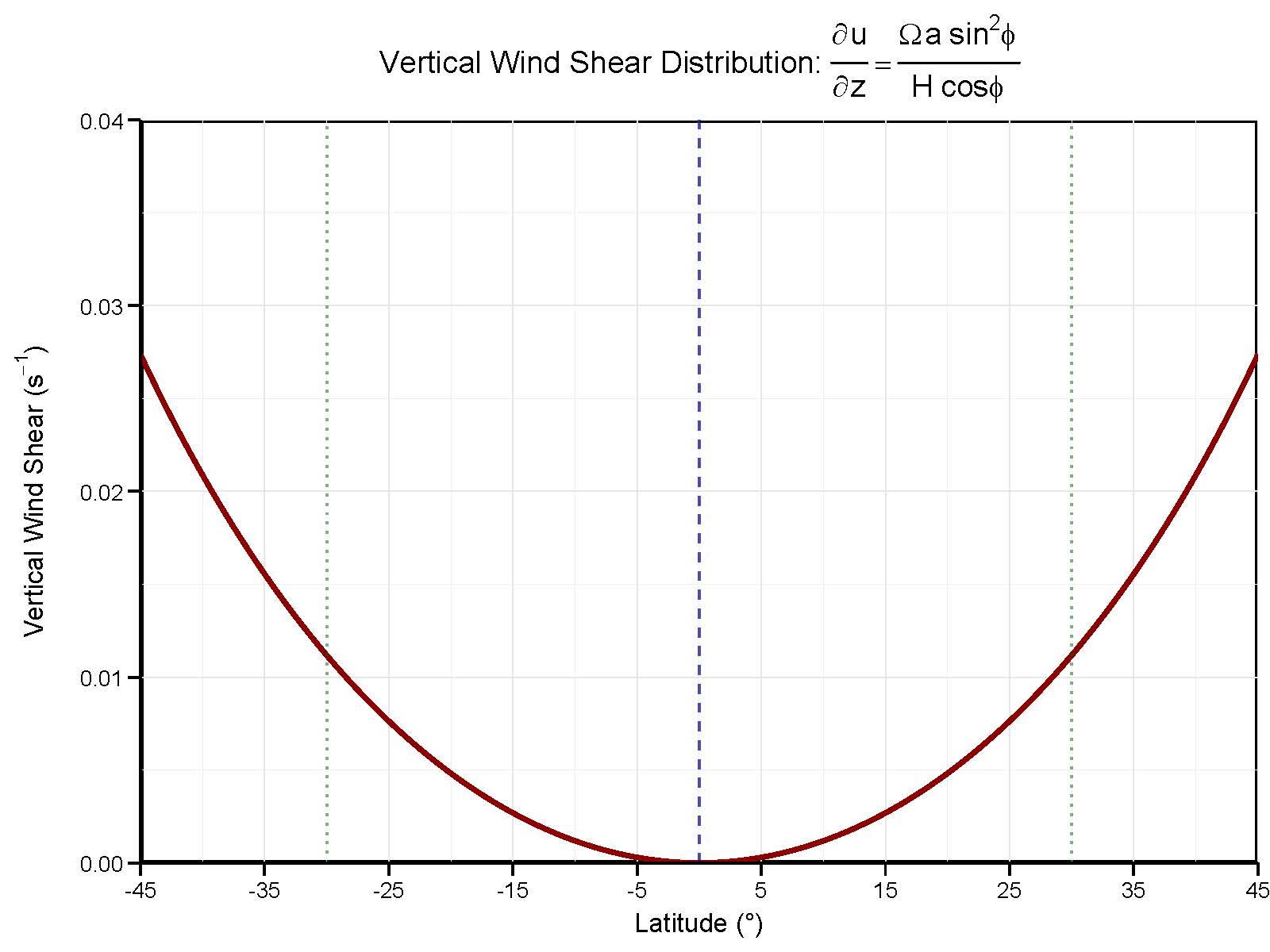
图 2.4 垂向风切变在正负45度内的变化，绿色虚线示意哈德利环流的平均南北界。图像使用R语言绘制，源码可在笔者的repository里找到（zonalshear.txt）。图形的分布完全对称，符合轴对称理论模型的假设。

事实上，垂向风切变存在与热成风（thermal wind）关系推导等价的导出方式。如果风在水平方向服从地转平衡，而压力在垂直方向服从流体静力平衡（hydrostatic balance），则会存在垂直风切变。这两种力平衡的组合称为热成风平衡：
$$
\tau = \frac{\partial u}{\partial z} = \frac{g}{2\Omega \sin\phi \cdot T_0} \frac{\partial T_M}{\partial y}\tag{2.8}
$$
其中， $\tau$ 为垂向风切变，$\Omega$ 为地球自转的角速度，$g$ 为重力加速度，$\phi$ 为纬度角，$T_0$ 为全球平均辐射平衡温度（太阳辐射下处于能量平衡状态下的地球整体的空间平均温度，与赤道温度不同），$2\Omega \sin\phi$ 是科氏参量 $f$（Coriolis parameter），式 2.8 的推导将在附录A给出。

联立式 2.7 和式 2.8 ，我们可以求得哈德利环流模型之下地球表面温度 $T_M$ 随沿经线方向远离赤道的距离 $y$ 的变化函数。考虑到地球上哈德利环流的影响范围较小，不妨对$\tau(\phi)$ 采用小角近似。这样，$\sin \phi$ 可以近似等于 $\frac{y}{a}$，而 $\cos \phi$ 可以近似等于1：
$$
\frac{\partial u}{\partial z} = \frac{\Omega y^2}{aH} = \frac{-g}{T_0 \cdot 2\Omega \cdot (y/a)} \cdot \frac{\partial T}{\partial y} = - \frac{ag}{yT_0 \cdot 2\Omega} \cdot \frac{\partial T}{\partial y}\tag{2.9}
$$

$$
\frac{\partial T}{\partial y} = \frac{\Omega g^2}{aH} \cdot \frac{yT_0 \cdot 2 \Omega}{ag}
= - \frac{2\Omega^2 T_0}{a^2 g H} y^3\tag{2.10}
$$

两边积分：
$$
T_{M} = - \frac{\Omega^2 T_0}{2a^2 g H} y^4 + T_{M0}\tag{2.11}
$$

其中 $T_{M_{0}}$ 表征哈德利环流情况下的赤道温度。根据我们的猜想，哈德利环流将潜热进行经向输送，那么，在全球辐射平衡的情况下，热带失去了多少热量，亚热带就要得到多少热量，也就是说，二者存在热平衡关系，净加热为0。数学上：
$$
\int_0^Y T_M \mathrm{d}y = \int_0^Y T_E \mathrm{d}y\tag{2.12}
$$
其中，Y是理论上哈德利环流的纬向界限， $T_{E}$ 是没有哈德利环流情况下的全球温度分布。后者的推导，需要构造一个纬度依赖的温度场（a latitude-dependent temperature field）。在没有哈德利环流的情况下，全球温度分布由当地辐射平衡决定，称为辐射平衡温度。

太阳辐射通量与纬度有关，地表接受的辐射通量近似为 $S_0 \cos\theta$，其中 $S_0$ 是太阳常数（约 1367 W/m²）（考虑地球表面积均摊），余纬度$\theta = 90^\circ - \phi$，其中 $\phi$ 是地理纬度。根据斯特藩-玻尔兹曼定律，地表向外辐射的能量正比于温度的四次方：
$$
S=\sigma T_E^4\tag{2.13}
$$

其中 $\sigma$ 是斯特藩-玻尔兹曼常数。假设地球为黑体，吸收的太阳辐射等于向外放出的辐射：
$$
S_0 (1 - \alpha) \cos\theta = \sigma T_E^4\tag{2.14}
$$

其中 $\alpha$ 是地球反照率（albedo，假设为常数）。由此，温度分布为：

$$
T_E(\theta) = \left( \frac{S_0 (1 - \alpha) \cos\theta}{\sigma} \right)^{1/4}\tag{2.15}
$$
这表明 $T_E$ 随 $\cos\theta$ 的四次方根变化，赤道温度最高，极地温度最低。

由于地球近似为球体，勒让德多项式（Legendare polynomial） $P_n(\sin\theta)$ 是球坐标系下描述轴对称物理量（如温度）自然的选择，因为它们是拉普拉斯方程在球面上的本征函数。辐射平衡温度的纬向分布呈现赤道热、极地冷的二次型特征，考虑第二阶勒让德多项式的正弦形式 $P_2(\sin\phi) = \frac{1}{2}(3{\sin^2\phi} - 1)$ 。

图 2.5 考虑勒让德多项式的低阶近似。上图给出了前六阶勒让德多项式的函数图像，符合辐射平衡温度的纬向分布的函数有且只有第二阶（绿线）。只需要用赤道温度$T_E(0)$扣去 $\sin \phi$ 的二阶勒让德多项式即可描述温度场在球面上的二次谐波分布，对应赤道加热和极地冷却的偶极子模式。（Fetched from Wikimedia, Licenced under GNU free protocol.）

$ T_E(\phi) $ 近似为勒让德多项式的二阶展开，考虑轴对称性（即温度仅依赖于纬度 $\phi$）：
$$
T_E(\phi) = a_0 P_0(\sin\phi) + a_2 P_2(\sin\phi)\tag{2.16}
$$
其中 $ P_0(\sin\phi) = 1 $ 是零阶项，代表全球平均温度；$ P_2(\sin\phi) $ 是第二阶勒让德多项式，描述纬向温度变化。设 $ a_0 = T_0 $，表示辐射平衡的基准温度（全球平均温度）。注意到 $ P_2(\sin\phi) $ 的值从 $-0.5(\phi=0)$ 到 $1(\phi=\pi/2)$，总变化为 1.5。温度差 $\Delta T$ 对应 $ P_2 $ 的变化，赤道到极地的温度降为 $\Delta T$。设总变化由 $1.5 a_2 $ 驱动，极地 ($ P_2 = 1 $) 比赤道 ($ P_2 = -0.5 $) 低 $\Delta T$：

$$
[(T_0 + a_2 \cdot 1) - (T_0 + a_2 \cdot (-0.5)] = \Delta T
$$
化简：

$$
a_2 = \frac{\Delta T}{1.5} = \frac{2}{3} \Delta T
$$

温度应从赤道到极地降低，无量纲的$ a_2 $ 应为负：
$$
a_2 = -\frac{2}{3} \Delta T\tag{2.17}
$$

代入 $ T_E(\phi) = T_0 + a_2 P_2(\sin\phi) $，其中 $ P_2(\sin\phi) = \frac{1}{2} (3 \sin^2 \phi - 1) $：

$$
T_E(\phi) = T_0 + \left(-\frac{2}{3} \Delta T\right) \cdot \frac{1}{2} (3 \sin^2 \phi - 1)
$$
化简：

$$
\boxed{T_E(\phi) = T_0 - \frac{1}{3} \Delta T (3 \sin^2 \phi - 1)}\tag{2.18}
$$

式 2.18 就是辐射平衡温度的表达式。将其套用小角近似：
$$
T_E(\phi) = \underbrace{T_{0} + \frac{1}{3}\Delta T}{T{E0}} - \Delta T \cdot \left(\frac{y}{a}\right)^2
$$

$$
\implies T_E=-\frac{\Delta Ty^2}{a^2}+T_{E0}\tag{2.19}
$$

其中$T_{E0}$是 $T_E(0)$ 的特解，对应没有哈德利环流情况下赤道的温度。考虑先前导出的哈德利环流存在情况下的温度函数（式 2.11）

$$
T_{M} = - \frac{\Omega^2 T_0}{2a^2 g H} y^4 + T_{M0}
$$

这样，哈德利环流的边界条件即为$T_E$与$T_M$的联立，对应哈德利环流的南北界：
$$
-\frac{\Delta Ty^2}{a^2}+T_{E0}=- \frac{\Omega^2 T_0}{2a^2 g H} y^4 + T_{M0}\tag{2.20}
$$
由于净加热为零（式2.12）
$$
\int_0^Y T_M \mathrm{d}y = \int_0^Y T_E \mathrm{d}y
$$
左边：
$$
\begin{align}
\int_0^Y T_M(y) \mathrm{d}y &= \int_0^Y \left( T_{M0} - \frac{\Omega^2 T_0}{2 a^2 g H} y^4 \right) \mathrm{d}y \
&= T_{M0} y - \frac{\Omega^2 T_0}{2 a^2 g H} \frac{y^5}{5} \Bigg|0^Y \
&= T{M0} Y - \frac{\Omega^2 T_0}{10 a^2 g H} Y^5
\end{align}\tag{2.21}
$$
右边：
$$
\begin{align}
\int_0^Y T_E(y) \mathrm{d}y &= \int_0^Y \left( T_{E0} - \frac{\Delta T}{a^2} y^2 \right) \mathrm{d}y \
&= T_{E0} y - \frac{\Delta T}{a^2} \frac{y^3}{3}\Bigg|0^Y \
&= T{E0} Y - \frac{\Delta T}{3 a^2} Y^3
\end{align}\tag{2.22}
$$
联立式2.21、式2.22，注意到两边都能消去一项 $Y$：
$$
T_{M0} - \frac{\Omega^2 T_0}{10 a^2 g H} Y^4 = T_{E0} - \frac{\Delta T}{3 a^2} Y^2\tag{2.23}
$$
联立边界条件（式2.20）和净加热积分（式2.23），得到哈德利环流的界限：
$$
\left( T_{M0} - \frac{\Omega^2 T_0}{2 a^2 g H} Y^4 \right) - \left( T_{M0} - \frac{\Omega^2 T_0}{10 a^2 g H} Y^4 \right)
= \left( T_{E0} - \frac{\Delta T}{a^2} Y^2 \right) - \left( T_{E0} - \frac{\Delta T}{3 a^2} Y^2 \right)
$$

$$
\implies \quad \frac{\Omega^2 T_0}{a^2 g H} \left( -\frac{4}{10} \right) Y^4 = \frac{\Delta T}{a^2} \left( -\frac{2}{3} \right) Y^2
$$

$$
i.e. \quad\boxed { Y =\sqrt \frac{5 \Delta T g H}{3 \Omega^2 T_0} }\tag{2.24}
$$

下面用式2.20求赤道地区的温度差（注意，式2.23是变形后消去Y的产物，没有严格的物理意义，在求没有系数的温度差时，不能用它！）：

$$
T_{E0} - T_{M0} = \frac{\Delta T}{a^2} Y^2 - \frac{\Omega^2 T_0}{2 a^2 g H} Y^4
$$

$$
Y^2 = \frac{5 \Delta T g H}{3 \Omega^2 T_0}, \quad Y^4 = \left( \frac{5 \Delta T g H}{3 \Omega^2 T_0} \right)^2
$$

$$
T_{E0} - T_{M0} = \frac{\Delta T}{a^2} \left( \frac{5 \Delta T g H}{3 \Omega^2 T_0} \right) - \frac{\Omega^2 T_0}{2 a^2 g H} \left( \frac{25 \Delta T^2 g^2 H^2}{9 \Omega^4 T_0^2} \right)
$$

$$
T_{E0} - T_{M0} = \frac{5 \Delta T^2 g H}{3 a^2 \Omega^2 T_0} - \frac{25 \Delta T^2 g H}{18 a^2 \Omega^2 T_0} = \frac{30 \Delta T^2 g H - 25 \Delta T^2 g H}{18 a^2 \Omega^2 T_0}
$$
即：
$$
\boxed{T_{E0} - T_{M0} = \frac{5 \Delta T^2 g H}{18 a^2 \Omega^2 T_0}}\tag{2.25}
$$

带入相关数据：

地球自转角速度：$\Omega = 7.3 \times 10^{-5}$ 弧度/s
地球半径：$a = 6371.4 , \text{km}$
对流层厚度：$H = 12 , \text{km}$
全球平均辐射平衡温度：$T_0 = 255 , \text{K}$
赤道-极地温度差异：$\Delta T = 100 , \text{K}$
重力加速度：$g = 9.8 , \text{m/s}^2$

解得 Y≈3797.8 km，$T_{E0} - T_{M0}$ ≈ 5.92 K。我们可以轻松地绘制两种情况下的温度分布：

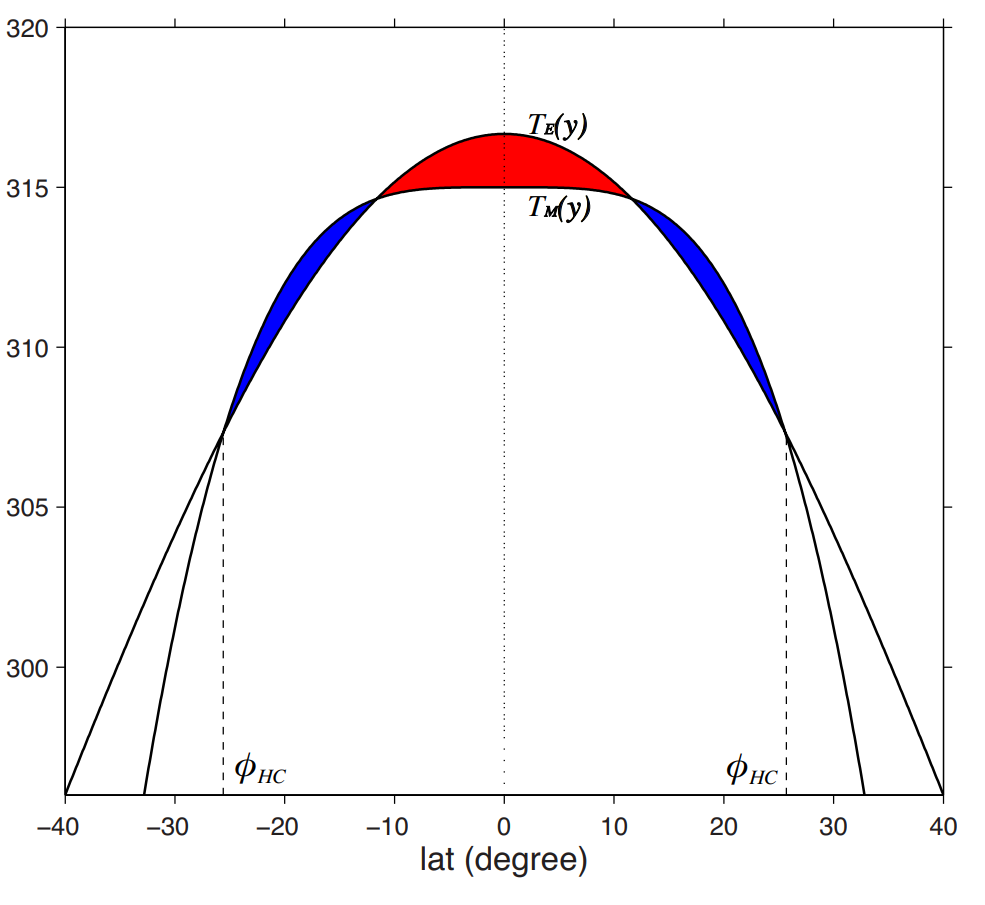
图 2.6 存在哈德利环流情况下的全球气温分布（$T_M$）和没有哈德利环流情况下的全球气温分布（$T_E$）。纵轴示温度，单位为K；$\phi_{HC}$示哈德利环流的南北两界，在此之外不存在哈德利环流带来的效应。蓝色部分表征哈德利环流给高纬方向带来的热量，红色部分表征哈德利环流在赤道带走的热量。左右两极的交点表征哈德利环流的南北界；中间的两个交点表征热量输送态的变化。（Lu et al., 2014）

Held-Hou 模型可以适用于辐射平衡温度的最大值不再位于赤道，而是在某个纬度 $\phi_0$ 处的情况。此时除需确定哈德利环流圈的南北边界纬度外，还需求解将环流分割为夏冬半球的分纬度 $\phi_C$ （该纬度与 $\phi_0$ 并不重合）。虽然代数运算稍显复杂，但其论证步骤与前一节描述的对称哈德利环流圈完全一致。

图 2.7 展示了计算结果。即使 $\phi_0$ 很小，夏季环流圈也会急剧收缩，而冬季环流圈则显著增强。环流强度可通过温度曲线与辐射平衡曲线之间的面积来表征：当 $\phi_0$ 仅为5°时，冬季环流圈强度较对称情形增强约10倍，而夏季环流圈则减弱相似倍数，这使得冬季环流强度可达夏季环流的约100倍。

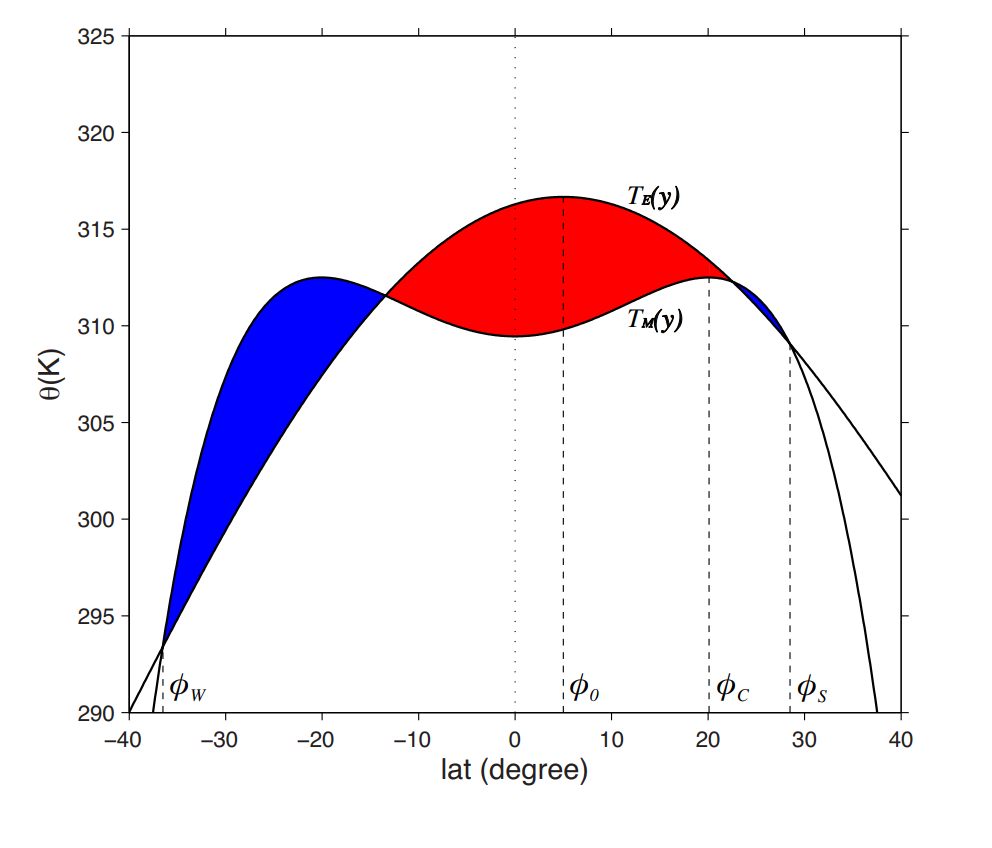
图 2.7 同图 2.6，但展示的是加热最大值偏离赤道的情况。其中 $\phi_0$ 表示辐射平衡温度最大值的纬度，$\phi_C$为划分冬季与夏季哈德莱环流圈的分界纬度，$\phi_W$和$\phi_S$分别代表冬季与夏季哈德莱环流圈的边界纬度。（Lu et al., 2014）

这种对最大加热纬度的高度非线性响应（non-linear response）意味着，年平均经向环流强度远大于由年平均加热场推导出的环流强度。这是气候研究中普遍存在的”非线性平均”问题的典型案例，同时也调和了Held-Hou模型的弱环流与观测到的强环流之间的矛盾：我们应将年平均环流理解为夏至和冬至时环流的平均态，而非对年平均热力辐射强迫的响应。

哈德利环流的变率

到目前为止，我们已经构建起了一个基本的、描述哈德利环流的模型。然而，地球大气违反了模型的基本假设：角动量并非始终守恒，热带大气也不是能量封闭系统。因此，Held-Hou 模型是一种概念性模型，无法对哈德利环流对大气参数变化的敏感性作出定量精确的预测。此前的大多数研究认为，Held和Hou提出的理论虽然聚焦热带热力学过程，但未能纳入实际大气中起关键作用的活动，因此无法准确预测哈德利环流的边界范围（Xian et al., 2021）。比如：

• 太平洋年代际振荡（PDO）在调制哈德利环流宽度中扮演重要角色。海温异常会通过改变热带和中纬度之间的热量输送，影响大气的斜压性：冷相位PDO通过改变海表温度（SST）分布，增强了副热带的经向温度梯度，从而促进哈德利环流边缘向极地扩展，尤其在春秋季节表现更为显著。（Grassi et al., 2012; Allen et al., 2014）。

• 外部强迫对哈德利环流的影响同样不容忽视。大型火山喷发通过向平流层注入气溶胶，导致平流层增温和对流层冷却，压低对流层顶高度，并可能触发厄尔尼诺事件。这种双重效应可使哈德利环流收缩约1个纬度。（Xian et al., 2021）

• 南极臭氧洞通过改变平流层热动力状态，增强副热带地区的斜压不稳定性（后面论述），导致环流边缘显著向极地移动。随着《蒙特利尔议定书》的实施，臭氧层的逐步恢复预计将部分抵消温室气体（GHG）引起的环流扩展效应，尤其在21世纪上半叶。温室气体浓度的增加通过吸收长波辐射，造成对流层增温和平流层冷却，抬升对流层顶高度，并通过增强副热带地区的静力稳定度削弱斜压性，从而推动哈德利环流边缘向极地方向移动。（Xian et al., 2021）

事实上，在Held的理论框架中，哈德利环流的边界范围可解释为由热成风平衡的条件，而非由热力环流的能量闭合条件决定。在全球变暖背景下，由于湿热力学过程导致的递减率改变——这会提升对流层静力稳定度（对流层顶高度）——使得哈德利环流极向侧翼的副热带急流达到斜压不稳定所需的稳定状态，从而驱动哈德利环流向极地扩展。如果直接反映到Held-Hou模型里，那就是式2.24中，分子H的增加会使得哈德利环流边界的极向移动。根据同样的思路我们能够讨论更多影响哈德利环流界限的因素。考察式2.24：
$$
Y =\sqrt \frac{5 \Delta T g H}{3 \Omega^2 T_0}
$$
其中，$g, \Omega$ 为常数，因此Y是 $\Delta T, H, T_0$ （赤道-极地温度差异、对流层顶高度、全球辐射平衡温度）的函数。我们把上面讨论的内容绘制成图表（图 2.8）。$\Delta T$ 和 $H$ 的增加、$T_0$ 的减少会导致 $Y$ 的增大，反之亦然。目前，温室气体的增加会使得对流层变暖，大气膨胀，使得对流层高度增加（增加的对流层高度）；人为气溶胶不均一的空间分布、自然海温随海气耦合作用的时空变化会导致气温梯度的改变（改变气温梯度），进而影响 $\Delta T$ 和 $T_0$ 。

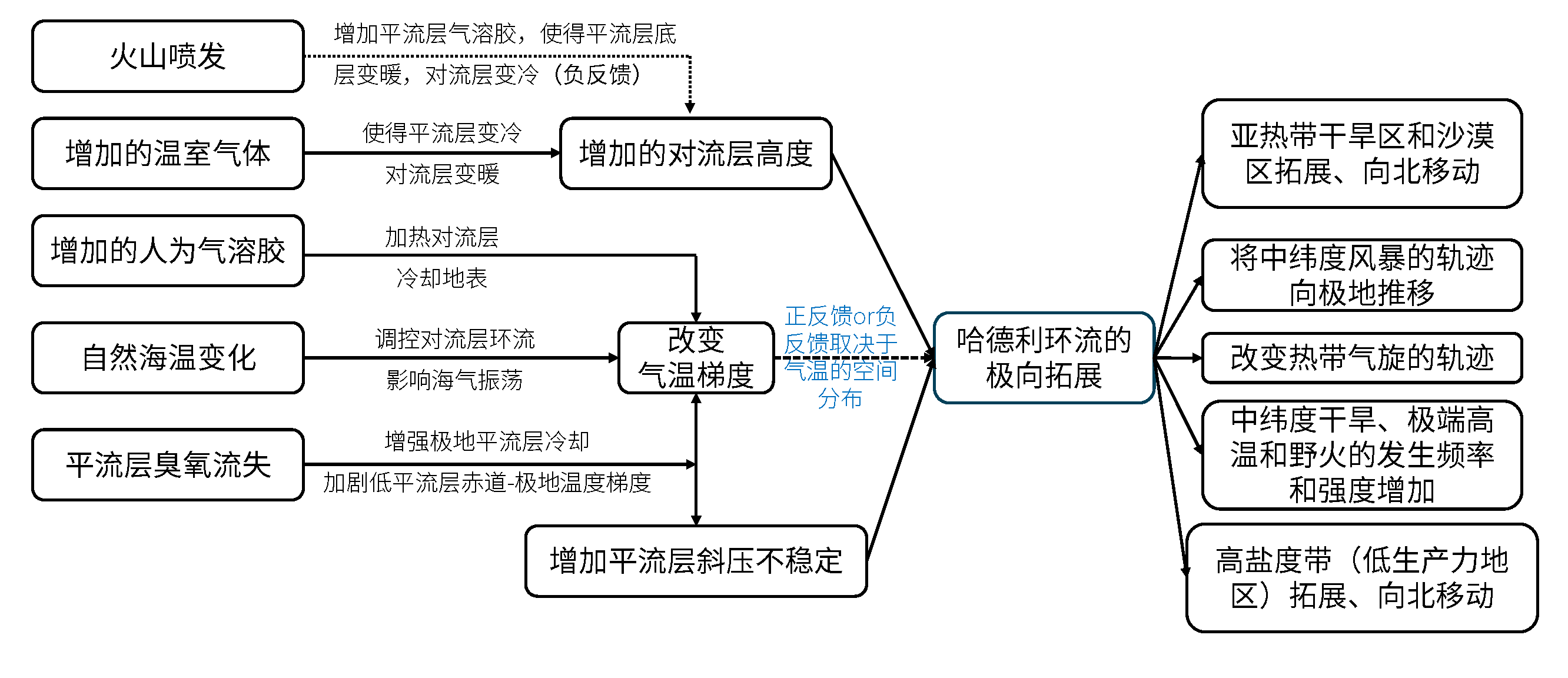
图2.8 影响哈德利环流拓展的因素和结果（改自Xian et al., 2021），讨论见上文。

斜压不稳定性（baroclinic instability）是大气中纬度地区天气系统形成和演变的核心机制，其根源在于热带与极地之间的经向温度梯度以及由此引发的垂直风切变。比如，当中纬度瞬变涡旋进入副热带时会扰乱角动量守恒流，导致高层纬向风速减弱，垂直风切变减小，进而降低斜压不稳定性（K. Seo et al., 2023）。2000年，Held 在伍兹霍尔海洋研究所的研讨会上指出，哈德利环流的宽度并非单纯由热力驱动环流的能量闭合决定，而是受限于温度依赖的风场在副热带地区变得斜压不稳定的纬度。

在全球变暖情景下，对流层增温增强了热带与中纬度之间的经向温度梯度，抬升了对流层顶高度，副热带急流的纬向风速得以在更高纬度维持，而不因斜压不稳定性而崩溃；温室气体浓度增加导致对流层增温和对流层顶冷却，温度递减率减小，静力稳定性增强。对流层顶高度的抬升进一步稳定了副热带急流，增强了低纬平流层的斜压不稳定性，使得哈德利环流可以在纬度更高的地区维持（Held, 2000; Xian et al., 2021）。

其他星球的哈德利环流

通过已经建立起来的 Held-Hou 模型，我们可以很容易地计算出其他类地行星上（甚至是地球历史时期）的哈德利环流边界。对于任意的行星，其哈德利环流边界由如下参数决定：自转角速度 $\Omega$、半径 $a$ 、对流层厚度 $H$ 、全球平均辐射平衡温度 $T_0 $ 、赤道-极地温度差异$\Delta T $ 和重力加速度 $g $。

正如地球大气一样，哈德利环流在这些类地行星的大气中也是主要的经向环流形式。 尽管目前了解较少，但在太阳以及系外行星的大气中也可能存在哈德利环流。哈德利环流的空间尺度可能取决于行星或卫星的自转速率——转速越快（$\Omega \Uparrow$），哈德利环流越紧缩（$Y\Downarrow$）。而转速越慢，地转偏向力效应减弱，从而减少了维持哈德利环流极向边界急流所需的经向温度梯度，使得哈德利环流得以进一步向极地延伸（Read, 2011）。接下来我们将以两颗星球：比邻星b（Proxima Centauri b）和土卫六（Titan）为类比，进行相关的实证分析。

比邻星b

参数	$\Omega$	$H$	$T_0$	$\Delta T$	$g$
值	$6.5\times10^{-6}\enspace\text{rad/s}$	15 km	234 K	~100 K	$10.6 ,\mathrm{m/s^2}$
参考文献	Faria et al., 2022; Galuzzo et al., 2021	Galuzzo et al., 2021	Anglada-Escudé et al., 2016	Del Genio et al., 2019；Galuzzo et al., 2021	Anglada-Escudé et al., 2016; Galuzzo et al., 2021 $M_p\approx 1.27, M_\oplus$ ;$R_p\approx 1.08, R_\oplus$

（假设潮汐锁定，自转周期等于公转周期（11.1869 d）；由于超旋转大气，$\Delta T$ 不是严格意义上的”赤道-两极温度差“。也就是说，比邻星上的哈德利环流是由向阳面的恒定日照驱动的。）

则带入式 2.24、式2.25，立刻得：
$$
Y_1 =\sqrt \frac{5 \Delta T g H}{3 \Omega^2 T_0}\approx5177.3 ,\text{km}\tag{2.26}
$$

$$
(T_{E0} - T_{M0})_1 = \frac{5 \Delta T^2 g H}{18 a^2 \Omega^2 T_0}\approx943,\text{K}\tag{2.27}
$$

由式2.26、2.27知，比邻星b有一个十分强大的哈德利环流系统，这意味着它能够高效地完成热量从永昼面向永夜面的经向输送，从而极大地改善其作为潜在宜居星球的条件。这种广域环流与海洋热输送协同作用，使得永夜面不会急剧降温，避免了大气塌缩与冰封情形的产生，令液态水得以维持 。也就是说，即便在对流弱化或天体潮汐锁定情况下，只要有足够的大气厚度或海洋储热，热量就能够被输送至背面，确保温度分布至少维持在使液态水存在的水平 （Faria et al., 2022）。上面的讨论与利用GCM模型计算的比邻星大气环流保持一致（图2.9）。

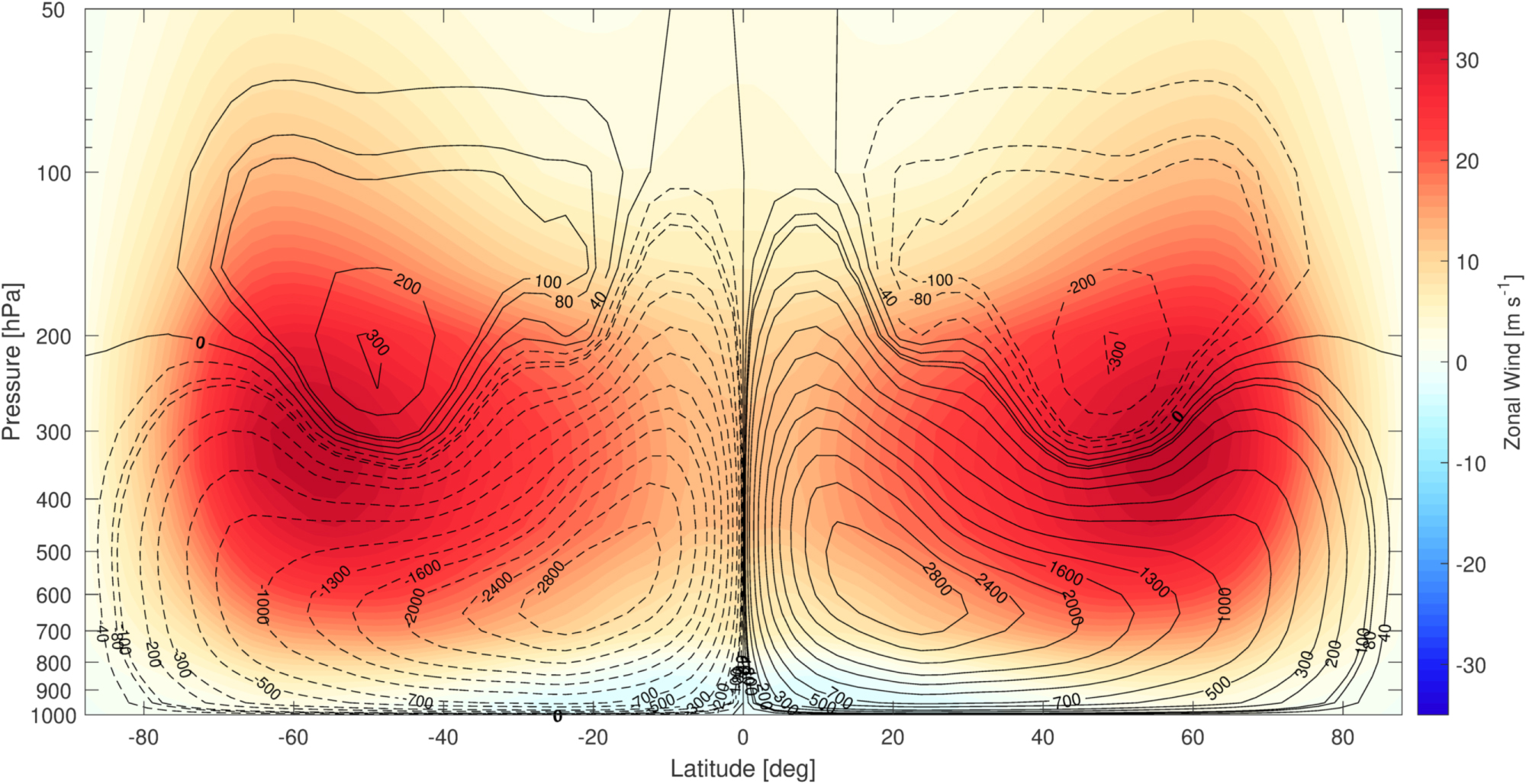
图 2.9 比邻星b的纬向风随纬度的分布，使用PlaSim软件完成。颜色代表纬向风的平均值，正值表示西风，负值表示东风。黑线表示质量流函数：实线表示顺时针环流（ψ > 0），虚线表示逆时针环流（ψ < 0）（Galuzzo et al., 2021）。可以看出比邻星b的纬向风从赤道一直延展至两极。需要注意的是比邻星b的太阳辐射由向阳面的恒定日照驱动，与纯粹Held-Hou模型（假设）的不均一性存在差异，因此式 2.27 存在数值过大的嫌疑。

土卫六

参数	$\Omega$	$H$	$T_0$	$\Delta T$	$g$
值	$4.56\times10^{-6}\enspace\text{rad/s}$	40 km	82 K	20 K	$1.35 ,\mathrm{m/s^2}$

（数据来源于 Mitchell and Lora 在 2016 年发表的综述）

计算得 Y≈3249.1 km，这甚至大于其半径（2575 km），说明土卫六缓慢的自转能支撑一个空间尺度广阔的哈德利环流。GCM的模拟结果显示，土卫六大气中存在显著的跨赤道哈德利环流。这种环流模式与惠更斯号探测器在登陆土卫六赤道附近时所观测到的经向风特征高度吻合，表明模型能够较好地捕捉其大气动力学特征。（Tokano, 2007）

土卫六上甲烷对流云的分布进一步揭示了其哈德利环流的动态特性。惠更斯号的观测表明，上升支主要位于夏季半球的中纬度地区，尤其是在纬度约40°处，云的频繁形成与地球上赤道辐合带（ITCZ）的上升运动机制存在相似之处。（Montmessin et al., 2006）

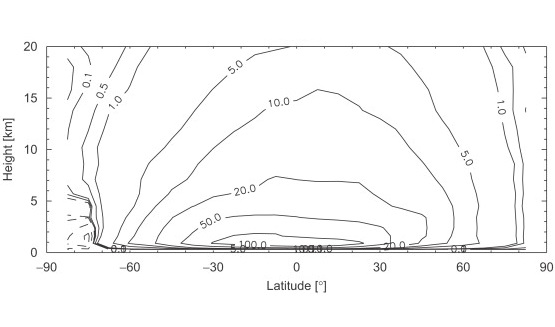
图 2.10 利用惠更斯号探测器收集的数据进行的GCM建模，实线是平均哈德利环流的质量流函数（单位：$10^{-8} \enspace\text{kg /s}$）。可以观察到，单一环流圈从南极一直延伸至北极。流线显示在几乎所有纬度2公里高度以下都存在向南流动，这代表了哈德利环流的下分支。整个南半球都出现上升运动，而北半球则出现下沉运动。（Tokano, 2007）

真题溯源

本组题目改编自 James, I.N. 在1994年出版的 Introduction to Circulating Atmospheres 一书的80-89页。作为大气动力学的经典教材，该部分讨论了哈德利环流的物理机制、Held-Hou模型和辐射变率。该教材在国内的许多大气科学系作为参考书使用。

图 2.11 Introduction to Circulating Atmospheres 书影。A：第80页（纬向的平均经向环流）；B. 第88页（有无哈德利环流情况下的温度分布，也就是题图22）；C. 第89页（对哈德利环流物理边界的讨论，也就是W9小问）。

相关资源：南大张洋老师的大气环流课程（包含部分课程资源）

附录A 热成风关系的推导

在研究大尺度大气和海洋运动时，地转偏向力是一个关键的惯性力，源于地球的自转。其中，科氏参数 $ f $ 定义为 $ f = 2\Omega \sin\phi $，其中 $ \Omega $ 是地球的自转角速度（约为 $ 7.292 \times 10^{-5} , \text{rad/s} $），$ \phi $ 是地理纬度。

在旋转坐标系中，地转偏向力对运动物体的影响表现为 $ \mathbf{F}_c = -2 \Omega \times \mathbf{v} $，其中 $ \mathbf{v} $ 是物体的速度向量。对于水平运动，假设速度为 $ (u, v, 0) $（分别沿经向和纬向），地球自转角速度向量 $ \mathbf{\Omega} $ 在局部坐标系中主要沿垂直方向（即纬度方向）的分量起作用。

在纬度 $ \phi $ 处，垂直分量为 $ \Omega \sin\phi $，因此地转偏向力的水平分量与 $ 2\Omega \sin\phi $ 成正比。具体而言，地转偏向力在纬向（y方向）对速度分量 $ u $（经向速度）的作用为 $ -f u $，其中 $ f = 2\Omega \sin\phi $。由此可知，在赤道（$ \phi = 0 $）时 $ f = 0 $，在极点（$ \phi = \pm 90^\circ $）时 $ f $ 达到最大。

在大尺度大气或海洋运动中，地转偏向力与气压梯度力（pressure gradient force）达到平衡，这就是地转平衡。在水平方向上，运动方程可以简化为地转偏向力与气压梯度力的平衡。对于纬向（y方向），气压梯度力由位势高度 $ \Phi $（或地球物理学中的位势，等于 $ g z $，其中 $ z $ 是高度，$ g $ 是重力加速度）的梯度决定，表达式为 $ -\frac{\partial \Phi}{\partial y} $。

在北半球（$ f > 0 $），地转偏向力对纬向速度 $ u $ 的作用为 $ -f u $，因此平衡方程为 $ -f u = -\frac{\partial \Phi}{\partial y} $，即
$$
f u = \frac{\partial \Phi}{\partial y}\tag{2A-1}
$$
这表明，纬向速度 $ u $ 与位势高度的纬向梯度成正比，且流向与等高线垂直，符合地转流的特征。将其带入
$$
f = 2\Omega \sin\phi\tag{2A-2}
$$
因此：
$$
u =\frac{1}{f} \frac{\partial \Phi}{\partial y}\tag{2A-3}
$$
由静力平衡（$\frac{\partial p}{\partial z} = -\rho g$）和理想气体状态方程（$ \rho = \frac{p}{R T}$）可知，
$$
\frac{\partial p}{\partial z} = -\frac{p g}{R T}
$$

定义位势高度$\Phi = g z$，得到
$$
\Phi = g z \ \Rightarrow \ dz = \frac{d\Phi}{g}
$$
因为
$$
\frac{\partial \Phi}{\partial p} = \frac{\partial \Phi}{\partial z} \cdot \frac{\partial z}{\partial p} = g \cdot \frac{\partial z}{\partial p}
$$
所以求倒数：
$$
\frac{\partial z}{\partial p} = \frac{1}{\partial p / \partial z} = -\frac{R T}{p g}
$$
带入，得
$$
\frac{\partial \Phi}{\partial p} = -\frac{R T}{p}\tag{2A-4}
$$
带入式 2A-3：
$$
\frac{\partial u}{\partial p} = \frac{R}{f p} \frac{\partial T}{\partial y}\tag{2A-5}
$$
转换为高度坐标，利用 $\frac{\partial p}{\partial z} = -\frac{p}{R T} g$：
$$
\frac{\partial u}{\partial z} = -\frac{g}{f T} \frac{\partial T}{\partial y}\tag{2A-6}
$$
带入 $f$：
$$
\boxed{\frac{\partial u}{\partial z} = -\frac{g}{2\Omega \sin\phi \cdot T} \frac{\partial T}{\partial y}\tag{2A-7}}
$$

即得式 2.8 。

参考文献

1. Allen, R.J., J.R. Norris, and M. Kovilakam, Influence of anthropogenic aerosols and the Pacific Decadal Oscillation on tropical belt width. Nature Geoscience, 2014. 7(4): p. 270–274.

2. Anglada-Escudé, G., et al., A terrestrial planet candidate in a temperate orbit around Proxima Centauri. Nature, 2016. 536(7617): p. 437–440.

3. Christopherson, R., 地表系统：自然地理学导论（原书第8版）. 2018, 北京: 科学出版社.

4. Del Genio, A.D., et al., Albedos, Equilibrium Temperatures, and Surface Temperatures of Habitable Planets. The Astrophysical Journal, 2019. 884(1): p. 75.

5. Diaz, H.F. and R.S. Bradley, The Hadley Circulation: Present, Past, and Future, in The Hadley Circulation: Present, Past and Future, H.F. Diaz and R.S. Bradley, Editors. 2004, Springer Netherlands: Dordrecht. p. 1–5.

6. Faria, J.P., et al., A candidate short-period sub-Earth orbiting Proxima Centauri★. A&A, 2022. 658.

7. Galuzzo, D., et al., Three-dimensional Climate Simulations for the Detectability of Proxima Centauri b. The Astrophysical Journal, 2021. 909(2): p. 191.

8. Grassi, B., et al., Effects of the PDO Phase on the Tropical Belt Width. Journal of Climate, 2012. 25(9): p. 3282–3290.

9. Held, I.M., The General Circulation of the Atmosphere, in 2000 Program in Geophysical Fluid Dynamics. 2000, Woods Hole Oceanographic Institution: Falmouth, MA, USA.

10. Held, I.M. and A.Y. Hou, Nonlinear Axially Symmetric Circulations in a Nearly Inviscid Atmosphere. Journal of Atmospheric Sciences, 1980. 37(3): p. 515–533.

11. Hudson, R.D., Measurements of the movement of the jet streams at mid-latitudes, in the Northern and Southern Hemispheres, 1979 to 2010. Atmos. Chem. Phys., 2012. 12(16): p. 7797–7808.

12. James, I.N., Introduction to Circulating Atmospheres. Cambridge Atmospheric and Space Science Series. 1994, Cambridge: Cambridge University Press.

13. Lu, J. and G. Vecchi, HADLEY CIRCULATION, in Encyclopedia of Atmospheric Sciences. 2014.

14. McKay, C.P., J.B. Pollack, and R. Courtin, The Greenhouse and Antigreenhouse Effects on Titan. Science, 1991. 253(5024): p. 1118–1121.

15. Mitchell, J.L. and J.M. Lora, The Climate of Titan. Annual Review of Earth and Planetary Sciences, 2016. 44(Volume 44, 2016): p. 353–380.

16. Persson, A.O., Hadley’s Principle: Understanding and Misunderstanding the Trade Winds. History of Meteorology, 2006. 3(3): p. 17–42.

17. Rannou, P., et al., The Latitudinal Distribution of Clouds on Titan. Science, 2006. 311(5758): p. 201–205.

18. Read, P.L., Dynamics and circulation regimes of terrestrial planets. Planetary and Space Science, 2011. 59(10): p. 900–914.

19. Seo, K.-H., et al., What controls the interannual variation of Hadley cell extent in the Northern Hemisphere: physical mechanism and empirical model for edge variation. npj Climate and Atmospheric Science, 2023. 6(1): p. 204.

20. Tokano, T., Near-surface winds at the Huygens site on Titan: Interpretation by means of a general circulation model. Planetary and Space Science, 2007. 55(13): p. 1990–2009.

21. Xian, T., et al. Is Hadley Cell Expanding? Atmosphere, 2021. 12, DOI: 10.3390/atmos12121699.

22. Hadley Cell. Available from: https://en.wikipedia.org/wiki/Hadley_cell.

---

封面图片：Earth atmosphere feb 26 2021 NASA ISS